Quadratische Pyramide berechnen

Wie man an einer geraden, quadratischen Pyramide rechnet, lernt ihr hier. Folgende Inhalte werden angeboten:

• Eine Erklärung, wie eine Pyramide aufgebaut ist.
• Beispiele und Formeln zum Rechnen an einer quadratischen Pyramide.
• Übungen damit ihr dies alles selbst üben könnt.
• Ein Video zum Rechnen an einer quadratischen Pyramide.
• Ein Frage- und Antwortbereich zu diesem Thema.

Tipp: Ihr tut euch sehr viel leichter beim Rechnen an einer Pyramide, wenn ihr ein paar Vorkenntnisse habt. Hilfreich ist es zum Beispiel, wenn ihr bereits den Satz des Pythgaoras, Fläche Rechteck und Volumeneinheiten kennt.

Quadratische Pyramide: Höhe, Seite, Fläche und Volumen

Sehen wir uns zunächst einmal an, wie eine gerade, quadratische Pyramide aussieht. Die nächste Grafik zeigt eine Pyramide mit einem Quadrat als Grundfläche.

Möchte man mit einer quadratischen Pyramide rechnen, dann sollte man einige wichtige Begriffe zu einer Pyramide kennen und es müssen passende Variablen festgelegt werden. Werft zunächst einen Blick auf die Pyramide mit Variablen (Buchstaben).

Wichtige Begriffe und Variablen:

• Grundfläche: Die Grundfläche ist der Boden. In unserem Fall ist die Grundfläche ein Quadrat. In Formeln wird diese Fläche oft mit "A_G" bezeichnet.
• Grundkante: Die Grundfläche hat am Boden vier Kanten (auch vier Seiten genannt). Diese werden als Grundkanten bezeichnet und in den Formeln oft mit "a" bezeichnet.
• Seitenkante: Von der Grundfläche gehen vier Seiten nach oben in die Spitze. Diese werden als Seitenkanten bezeichnet. In den Gleichungen werden diese mit "s" eingesetzt.
• Höhe: Eine Pyramide hat eine Höhe (auch Körperhöhe genannt). Dabei ist die maximale Höhe gemeint welche in Gleichungen mit "h" bezeichnet wird.
• Seitenhöhe: Geht man von der Mitte einer Grundkante nach oben, gelangt man über eine Seite in die Spitze. Die Länge einer Seitenhöhe wird mit "h_s" oder "h_a" bezeichnet.
• Mantelfläche: Die Pyramide hat runderum vier Flächen. Eine Fläche vorne, eine Fläche hinten sowie die Flächen links und rechts. Die Größe der Mantelfläche wird mit "A_M" bezeichnet.
• Oberfläche: Die Oberfläche (Oberflächeninhalt) ist die Summe aus der Grundfläche plus der Mantelfläche. Sie wird in Formeln "A_O" oder "O" genannt.
• Volumen: Wie viel Inhalt in die Pyramide passt wird mit dem Volumen angegeben. In der Formel ist dies meistens ein "V".

Formeln quadratische Pyramide:

Anzeige:

Beispiel quadratische Pyramide

In diesem Abschnitt sehen wir uns ein Beispiel an wie man eine quadratische Pyramide berechnet.

Beispiel 1: quadratische Pyramide

Wir haben eine gerade quadratische Pyramide. Diese hat eine Grundkante von 240 Meter und eine Seitenkante von 220 Meter. Wie hoch ist die Pyramide? Wie groß ist eine Seitenhöhe? Wie groß ist die gesamte Oberfläche und das Volumen dieser Pyramide?

Lösung:

Dem Text entnehmen wir, dass die Grundkante a = 240 m ist. Außerdem ist die Seitenkante s = 220 m. Wir möchten die Höhe h und die Seitenhöhe h_s berechnen. Im Anschluss suchen wir noch die gesamte Oberfläche A_G und das Volumen V. Wer jetzt einfach in die Formeln einsetzen möchte, merkt jedoch schnell, dass in einer Gleichung durchaus mehrere Unbekannte (Variablen) vorkommen für die wir keine Angaben haben.

Da wir jedoch s = 220 m und a = 240 m kennen, können wir die letzte Gleichung aus unserer Formelsammlung von oben anwenden. Beachtet dabei, dass sowohl die Zahl als auch die Einheit quadriert werden müssen, daher wird beim Einsetzen stets eine Klammer gesetzt. Wir rechnen dies aus und fassen unter der Wurzel zusammen.

Quadratische Pyramide h berechnen:

Wir erhalten eine Höhe von 140 Meter für die Pyramide. Für weitere Rechnungen merken wir uns h = 140 m. Mit dieser Angabe gehen wir in die nächste Gleichung um die Seitenhöhe h_s zu berechnen.

Quadratische Pyramide h_s berechnen:

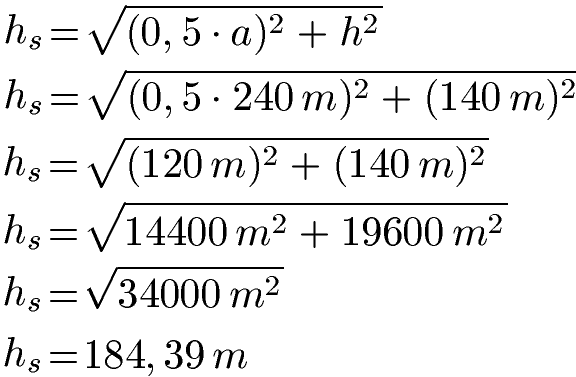
Die Seitenlänge beträgt damit 184,39 Meter. Wir merken uns h_s = 184,39 m. Im nächsten Schritt berechnen wir die Grundfläche A_G mit der Grundkante a = 240 m.

Quadratische Pyramide Grundfläche berechnen:

Wir kennen jetzt die Grundfläche von A_G = 57600 m². Fehlt uns noch die Mantelfläche A_M:

Quadratische Pyramide Mantelfläche berechnen:

Mit der Grundfläche (Bodenfläche) und der Mantelfläche können wir die Gesamtfläche / Oberfläche berechnen.

Quadratische Pyramide Oberflächeninhalt berechnen:

Die Oberfläche der Pyramide liegt bei A_O = 146107,2 m².Mit der Grundfläche und der Höhe berechnen wir das Volumen.

Quadratische Pyramide Volumen berechnen:

Das Volumen der Pyramide beträgt 2688000 m³.

Aufgaben / Übungen quadratische Pyramide

Aufgabe 1:

Bevor wir rechnen eine kurze Frage:

• Wie nennt man so eine Pyramide?

• Parallelpyramide
• quadratische Pyramide
• Kreispyramide
• runde Pyramide

Weiter zur Lösung » Aufgabe überspringen »

Du hast 0 von 5 Aufgaben erfolgreich gelöst.

Anzeigen:

Video quadratische Pyramide

Fragen mit Antworten quadratische Pyramide