Kreiszahl Pi

Was die Kreiszahl π (gesprochen: pi) ist, lernt ihr hier. Dies sehen wir uns an:

• Eine Erklärung was die Kreiszahl π ist.
• Beispiele um die Kreiszahl zu berechnen, auch per Hand.
• Aufgaben / Übungen damit ihr dies selbst üben könnt.
• Ein Video zum Rechnen am Kreis.
• Ein Frage- und Antwortbereich zu diesem Thema.

Tipp: Zur Kreiszahl braucht ihr eigentlich keine großen Vorkenntnisse. Es hilft jedoch wenn ihr ganz einfache Gleichungen auflösen könnt.

Erklärung Kreiszahl

Die Kreiszahl benötigt man oft beim Rechnen am Kreis. Sie hilft Umgang und Fläche zu berechnen. Die Kreiszahl wird dabei mit einem π abgekürzt. Gesprochen wird dies pi. Es handelt sich dabei um eine Konstante, sprich um eine Zahl, dies sich nicht verändert.

Die Kreiszahl π ist eine unendlich lange Zahl, sprich es gibt unendlich viele Stellen nach dem Komma. Sie ist nicht als Bruch darstellbar. In der Praxis verwendet man daher eine abgekürzte Darstellung der Zahl:

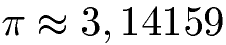
Das "geschwungene" Istgleich-Zeichen wird mit "ungefähr" ausgesprochen. Wie kann man diese Zahl berechnen? Dies geht zum Beispiel mit dieser Gleichung:

Dabei ist:

• "π" ist die Kreiszahl, ungefähr 3,14159
• "U" ist der Umfang vom Kreis
• "d" ist der Durchmesser vom Kreis

Beispiel 1: Formel Kreiszahl

Der Durchmesser von einem Kreis sei 10 cm und der Umfang sei 31,4159 cm. Wie groß ist Pi?

Lösung:

Wir setzen beide Angaben in die Gleichung ein und berechnen damit (den abgekürzten Wert) von Pi. Wichtig: Die Kreiszahl hat keine Einheit.

Wie kann man sonst noch auf die Kreiszahl kommen? Es gibt ganz viele Möglichkeiten auf diese zu kommen. Im nächsten Abschnitt sehen wir uns eine einfache Vorgehensweise an.

Anzeige:

Beispiel Kreiszahl zeichnerisch

Sehen wir uns eine einfache Möglichkeit an die Kreiszahl zu ermitteln.

Beispiel 2: Kreiszahl zeichnerisch

Mit einem Zirkel zeichnen wir uns einen möglichst großen Kreis auf Papier.

Wir messen den Durchmesser vom Kreis. In diesem Beispiel lesen wir am Geodreieck einen Durchmesser von 14 cm ab. Damit ist d = 14 cm.

Fehlt uns noch der Umfang. Dabei können wir nicht einfach den Umfang mit einem Geodreieck messen, sondern müssen uns anders helfen. Wir zeichnen gerade Linien in den Kreis ein, so wie in der nächsten Grafik gezeigt:

Jede grüne Linie ist etwa 5,8 cm lang und es sind 8 grüne Linien. Damit würden wir auf einen Umfang von U = 5,8 cm · 8 = 46,4 cm kommen. Wir setzen beides in die Gleichung ein und rechnen damit die Kreiszahl aus:

Mit dieser Methode kommen wir schon recht nahe an die echte Kreiszahl ran.

Aufgaben / Übungen Kreiszahl

Aufgabe 1: Wie groß ist Pi etwa?

• 2,9841
• 3,14159
• 3,0478
• 1,872

Weiter zur Lösung » Aufgabe überspringen »

Du hast 0 von 4 Aufgaben erfolgreich gelöst.

Anzeigen:

Video Kreis

Fragen mit Antworten Kreiszahl