Raute ▷ Formeln, Eigenschaften und Beispiele
Geschrieben von: Dennis RudolphDonnerstag, 19. Mai 2022 um 12:04 Uhr
Mit der Raute der Mathematik befassen wir uns in diesem Artikel. Dies sind die Themen:
- Eine Erklärung was eine Raute ist.
- Formeln und Beispiele zum Berechnen einer Raute.
- Ein Frage- und Antwortbereich zur Raute.
Hinweis: Die Raute ist eines von vielen Vierecken. Falls du noch weitere kennen lernen möchtest, findest du diese unter Vierecke der Mathematik.
Raute Eigenschaften und Formeln
Eine Raute hat folgende Eigenschaften:
- Alle vier Seiten sind gleich lang.
- Es gibt vier Eckpunkte (A, B, C und D).
- Es gibt zwei Diagonale ("e" und "f").
- Es gibt vier Innenwinkel (Alpha, Beta, Gamma und Delta).
- Die Diagonalen stehen im rechten Winkel (= orthogonal) zueinander.
- Die Diagonalen halbieren jeden Innenwinkel.
Die Eckpunkte werden entgegen dem Uhrzeigersinn beschriftet.
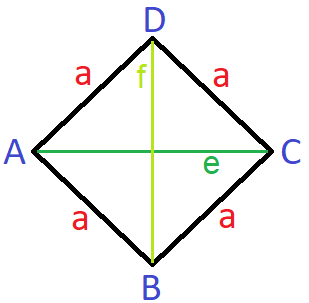
Die vier Winkel werden wie folgt angegeben:
- Am Eckpunkt A befindet sich der Winkel Alpha.
- Am Eckpunkt B befindet sich der Winkel Beta.
- Am Eckpunkt C befindet sich der Winkel Gamma.
- Am Eckpunkt D befindet sich der Winkel Delta.
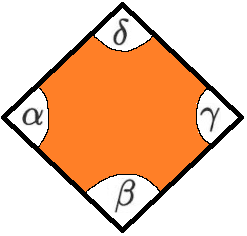
Raute Formeln:
Die Formeln zur Raute dienen dazu den Umfang "U" zu berechnen, den Flächeninhalt "A" oder die vier Winkel.
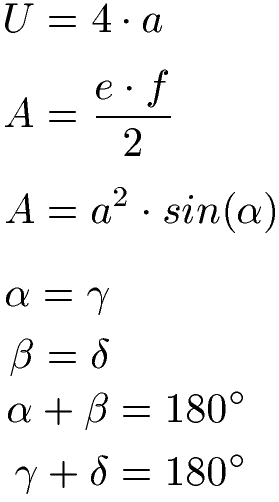
Ab dem nächsten Abschnitt sehen wir uns das Rechnen mit den Formeln der Raute an.
Anzeige:
Anzeigen:
Raute Umfang mit Beispiel
Unter dem Umfang eines Vierecks versteht man ein Mal um das Viereck herum zu laufen. Die Raute ist dabei ein spezielles Viereck: Eine Raute hat vier gleich lange Seiten, daher ist der Umfang das Vierfache einer Seite.
Um den Umfang auszurechnen wird daher eine der Seitenlängen mit 4 multipliziert. Als Beispiel nehmen wir eine Seitenlänge von 5 Metern. Wie groß ist der Umfang? Wir multiplizieren die 5 Meter mit 4.
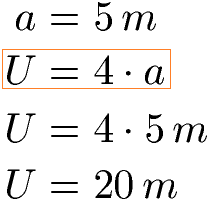
Der Umfang einer Raute mit 5 Metern Seitenlänge beträgt 20 Meter.
Raute Flächeninhalt mit Beispiel
Es gibt zwei Möglichkeiten den Flächeninhalt einer Raute zu berechnen:
- Die beiden Diagonalen multiplizieren und das Ergebnis halbieren.
- Eine Seitenlänge quadrieren und mit dem Sinus des Winkels Alpha multiplizieren.
Flächeninhalt über die Diagonalen:
Die Diagonalen einer Raute sind 4 Meter und 5 Meter lang. Wie groß ist die Fläche der Raute? Zur Lösung multiplizieren wir die Diagonalen miteinander und halbieren das Ergebnis.
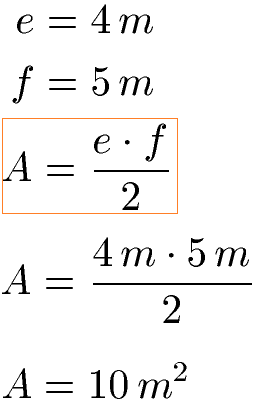
Eine Raute mit den Diagonalen 4 Meter und 5 Meter hat einen Flächeninhalt von 10 Quadratmetern.
Flächeninhalt über Winkel:
Sind die Seitenlängen und der Winkel Alpha bekannt kann darüber der Flächeninhalt berechnet werden. Als Beispiel sei a = 3 m und Alpha = 60 Grad. Die Formel sieht vor die Seitenlänge zu quadrieren. Außerdem muss der Sinus von 60 Grad berechnet werden. Verwende dazu den Taschenrechner, den du auf DEG stellen musst.
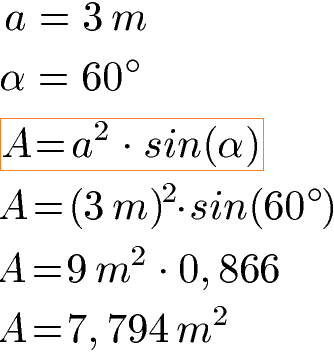
Fragen mit Antworten zur Raute
In diesem Abschnitt sehen wir uns typische Fragen mit Antworten zur Raute an.
Ist ein Quadrat auch eine Raute?
Ja, ein Quadrat ist eine Raute. Das Quadrat ist eine spezielle Raute, denn alle vier Innenwinkel sind 90 Grad groß. Bei der Raute können die Winkel auch andere Größen haben.
Was ist der Unterschied zwischen Raute und Quadrat?
Der Unterschied zwischen Raute und Quadrat liegt in den Winkeln. Ein Quadrat hat nur 90 Grad Winkel, eine Raute kann 90 Grad Winkel haben, muss es aber nicht.
Hat eine Raute 90 Grad?
Eine Raute kann 90 Grad Innenwinkel haben. Dies muss jedoch nicht sein.
Sind Raute und Parallelogramm dasselbe?
Nein, Raute und Parallelogramm sind nicht dasselbe. Bei Rauten sind alle vier Seiten gleich lang, beim Parallelogramm muss dies nicht so sein.
Welche Parallelogramme sind auch Rauten?
Ein Parallelogramm ist eine Raute wenn allen Seiten des Parallelogramms gleich lang sind.
Wie erkannt man eine Raute?
Eine Raute erkennst du daran, dass es ein Viereck mit vier gleich langen Seiten ist.
Neue Artikel
- Raute ▷ Formeln, Eigenschaften und Beispiele
- Sachaufgaben Klasse 5 Mathematik Aufgaben
- Sachaufgaben Mathe: Klasse 5
- Worte in Zahlen Aufgaben (Übungen)
- Worte in Zahlen umwandeln
- Teilerfremdheit (Mathematik)
- Hohlmaße umrechnen
- Hundertertafel Grundschule
- Quersumme berechnen und Teilbarkeit
- Quadratzahlen berechnen (mit Liste)
