Teilerfremdheit (Mathematik)

Was teilerfremd bedeutet und wie du dies berechnet, lernst du hier. Dies sind die Themen:

• Eine Erklärung was Teilerfremdheit ist.
• Beispiele um Zahlen auf Teiler zu überprüfen.
• Aufgaben / Übungen zu Teiler und Teilerfremdheit.
• Ein Video zu Teilern von Zahlen.
• Ein Frage- und Antwortbereich zu diesem Gebiet.

Hinweis: Es ist sehr hilfreich, wenn du weißt was der Teiler einer Zahl ist und zumindest die Teiler für kleine Zahlen bis 50 berechnen kannst. Falls du dir dabei noch unsicher bist, so wirf bitte erst einmal einen Blick auf die Inhalte unter Teiler und Vielfache.

Erklärung zu teilerfremd

Zwei Zahlen heißen teilerfremd, wenn sie keine gemeinsamen Teiler außer der Zahl 1 haben. Die Erklärung zur Teilerfremdheit lässt sich sehr einfach mit den Zahlen 7 und 11 verstehen. Beide Zahlen sind Primzahlen, haben also nur die Zahl 1 und sich selbst als Teiler. Daher sind 7 und 11 zueinander teilerfremd.

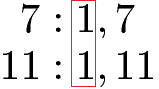
Um zu prüfen, ob zwei (oder mehr) Zahlen teilerfremd sind, können verschiedene Testverfahren eingesetzt werden. Für kleine Zahlen können die Teiler in einer Zahlenreihe aufgeschrieben werden. Die Zahl 8 lässt sich zum Beispiel durch 1, 2, 4 und 8 ohne Rest teilen. Ebenso können die Teiler der 12 ermittelt werden. Am einfachsten ist es, wenn man die Zahlenreihen untereinander schreibt.

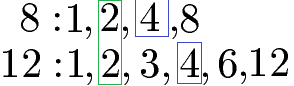
Wie hier auffällt, gibt es die Zahlen 2 und 4 zusätzlich als gemeinsame Teiler. Da es neben der 1 weitere Teiler gibt sind 8 und 12 nicht teilerfremd.

Anzeige:

Teilerfremd überprüfen Beispiele

Mit Zahlenreihen können sehr einfach kleine Zahlen nach Teilern untersucht werden. Je größer die Zahlen werden, desto schwieriger ist es, die Teiler mit den Teilbarkeitsregeln schnell zu ermitteln. Für große Zahlen wird daher die Primfaktorzerlegung eingesetzt. Die Primfaktorzerlegung dient dazu aus einer Zahl ein Produkt aus Primzahlen zu erzeugen.

Als Beispiel sollen einmal die Zahlen 99 und 132 auf Teilerfremdheit überprüft werden. Dazu zerlegen wir zunächst die 99 in Multiplikationen aus möglichst kleinen Zahlen, in diesem Fall den Primzahlen 3 und 11. Das Ergebnis schreiben wir als Potenz.

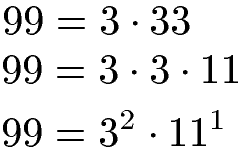
Die 132 wird ebenfalls in eine Multiplikation aus Primzahlen zerlegt. Wir erhalten dabei 2 Mal die 2, 1 Mal die 3 und 1 Mal die 11. Dieses Ergebnis bringen wir ebenfalls in die Potenzschreibweise.

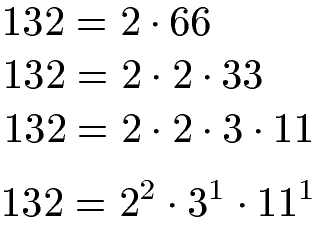
Zur besseren Übersicht schreiben wir uns die Primfaktorzerlegung in Potenzen für beide Zahlen noch einmal untereinander.

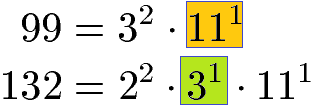
Um den größten gemeinsamen Teiler (ggT) zu finden suchen wir aus beiden Primfaktorzerlegungen die Potenzen mit gleicher Basis raus. Die Basis 2 gibt es nur bei 2². Daher spielt diese für das ggT keine Rolle. Die Basen 3 und 11 kommen jedoch in beiden Zerlegungen vor. Uns interessiert jeweils die kleinere Potenz, daher nehmen wir 3¹ und nicht 3² sowie 11¹.

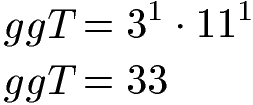
Der größte gemeinsame Teiler von 99 und 132 ist die Zahl 33. Sind Zahlen teilerfremd ist der größte gemeinsame Teiler die Zahl 1. Dies ist hier nicht der Fall, daher sind 99 und 132 keine teilerfremde Zahlen, sprich es gibt neben der 1 gemeinsame Teiler.

Aufgaben (Übungen) zu Teilern

Aufgabe 1: Wie lauten die ersten fünf Vielfachen von 4?

• 4, 9, 12, 16, 20
• 4, 8, 12, 16, 22
• 5, 8, 16, 16, 20
• 4, 8, 12, 16, 20

Weiter zur Lösung » Aufgabe überspringen »

Du hast 0 von 6 Aufgaben erfolgreich gelöst.

Anzeigen:

Fragen mit Antworten zu teilerfremd