Potenzregeln, Potenzgesetze, Potenzen vereinfachen

Die Potenzregeln (Potenzgesetze) und wie man Potenzen vereinfacht sehen wir uns hier an. Dies zeigen wir euch:

• Eine Erklärung welche Potenzregeln es gibt und wie man sie anwendet.
• Viele Beispiele zum Umgang mit den Potenzgesetzen.
• Aufgaben / Übungen damit ihr dies selbst üben könnt.
• Videos zum Umgang mit Zahlen bei der Potenzrechnung.
• Ein Frage- und Antwortbereich zu diesem Thema.

Wer noch gar keine Ahnung hat was eine Potenz überhaupt ist sieht bitte erst einmal in den Artikel Potenzen rechnen. Ansonsten sehen wir uns nun zahlreiche Regeln zu Potenzen an.

Erklärung Potenzregeln / Potenzgesetze

Die Potenzregeln bzw. Potenzgesetze dienen dazu mit Potenzen zu rechnen und Potenzen zu vereinfachen. Dazu zeige ich das jeweilige Potenzgesetz, sage wann man dieses verwendet und rechne ein Beispiel mit Zahlen vor. Zur besseren Übersicht sind diese durchnummeriert.

Potenzgesetz Nr. 1:

Die erste Potenzregel wird verwendet, wenn zwei Potenzen miteinander multipliziert werden. Dabei muss die Basis - also die große Zahl unten - jeweils gleich sein. Die Vereinfachung sieht so aus, dass man die Basis beibehält und die beiden Exponenten addiert.

Zum besseren Verständnis setzen wir ein paar Zahlen ein. Als Beispiel soll a = 2, n = 3 und m = 4 eingesetzt und berechnet werden. Wir vereinfachen dabei mit den Regeln zu den Potenzen und berechnen das Ergebnis.

Potenzgesetz / Potenzregel Nr. 2:

Die zweite Regel zum Rechnen mit Potenzen wird eingesetzt wenn die Exponenten (Hochzahlen) gleich sind, aber die Basen verschieden sind. Dabei werden die beiden Potenzen miteinander multipliziert. Man kann dies vereinfachen indem man die beiden Basen multipliziert und als Exponent die gemeinsame Hochzahl verwendet. Die Gleichung zum Vereinfachen sieht so aus:

Setzen wir zum Beispiel a = 4, b = 3 und n = 2 ein ergibt sich:

Potenzgesetz / Potenzregel Nr. 3:

Beim dritten Potenzgesetz geht es darum Potenzen zu potenzieren und diese zu vereinfachen. Dies geschieht indem man einfach die jeweiligen Exponenten miteinander multipliziert. Wie immer zunächst die Formel und im Anschluss ein Beispiel mit Zahlen.

Als Beispiel setzen wir wieder Zahlen ein, in diesem Fall a = 5, n = 2 und m = 3. Damit sieht die Rechnung so aus:

Anzeige:

Beispiele Potenzregeln

Wir hatten eben drei sehr oft benutzte Potenzgesetze. Jedoch sollen euch die folgenden nicht vorenthalten werden.

Potenzregeln / Potenzgesetze Nr. 4:

Die vierte Regel befasst sich mit Potenzregeln für einen Bruch. Wir haben dabei sowohl im Zähler als auch im Nenner eine Potenz. Die Exponenten sind dabei gleich. Das Vereinfachen sieht so aus, dass man die beiden Basen durcheinander dividiert und den gemeinsamen Exponenten als Hochzahl verwendet. Die allgemeine Gleichung sieht so aus:

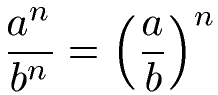
Zum besseren Verständnis erneut ein Beispiel: Wir setzen a = 3, b = 5 und n = 2 ein. Damit sieht die Berechnung so aus:

Potenzregeln / Potenzgesetze Nr. 5:

Das fünfte Potenzgesetz befasst sich ebenfalls mit Brüchen. Dieses geht davon aus, dass die Basis der Potenzen im Zähler und im Nenner gleich sind. Ist dies der Fall dann kann man vereinfachen, indem man die Basis beibehält und die Exponenten subtrahiert.

Setzen wir erneut ein paar Zahlen ein. Für die Basis nehmen wir a = 5 so wie n = 3 und m = 2. Damit sieht die Berechnung so aus:

Aufgaben / Übungen Potenzgesetze

Aufgabe 1: Bevor wir rechnen. Was ist eine Potenz?

• Abkürzung für Subtraktion
• Abkürzung für Division
• Abkürzung für Addition
• Abkürzung für Multiplikation

Weiter zur Lösung » Aufgabe überspringen »

Du hast 0 von 9 Aufgaben erfolgreich gelöst.

Anzeigen:

Potenzgesetze Video

Fragen mit Antworten zu Potenzregeln