kgV: kleinstes gemeinsames Vielfaches

Mit dem kleinsten gemeinsamen Vielfachen - kurz kgV - befassen wir uns hier. Dies sehen wir uns an:

• Eine Erklärung, was das kgV ist und wie man es berechnet.
• Viele Beispiele zur kgV-Berechnung, auch mit Primfaktorzerlegung.
• Aufgaben / Übungen rund zum kleinsten gemeinsamen Vielfachen.
• Ein Video zum Thema.
• Ein Frage- und Antwortbereich zu diesem Gebiet.

Tipp: Falls ihr Verständnisprobleme mit diesem Artikel habt, dann klemmt es vielleicht bei den Vorkenntnissen. Falls dem so ist seht erst einmal auf die Inhalte Multiplikation von Zahlen und Primfaktorzerlegung.

Erklärung kgV

Es kommt in der Mathematik nicht sonderlich oft vor, dass der Name von etwas schon beschreibt, was gesucht ist. Beim kleinsten gemeinsamen Vielfachen - kurz kgV - ist dies jedoch der Fall. Es handelt sich dabei um die kleinste natürlich die Zahl die vielfache zweier (oder mehr) von Ausgangszahlen ist. Es gibt mehrere Möglichkeiten der Berechnung. Die erste Variante ist einfach die Vielfachen der Zahlen aufzuschreiben und die kleinste gemeinsame Zahl zu finden.

Beispiel 1:

Von den Zahlen 3 und 5 soll das kgV ermittelt werden. Wie lautet dieses?

Lösung:

Wir multiplizieren zunächst beide Zahlen mit 1, 2, 3, 4, 5 usw. Dadurch erhalten wir die Vielfachen von 3 und 5.

Nun suchen wir aus den beiden Zahlenreihen die kleinste gemeinsame Zahl raus.

Das kleinste gemeinsame Vielfache von 3 und 5 ist damit 15.

Beispiel 2:

Im zweiten Beispiel soll der kleinste gemeinsame Vielfache der Zahlen 5, 8 und 12 ermittelt werden. Damit ist das kgV von drei Zahlen gesucht.

Lösung:

Wir bilden zunächst die Vielfachen von 5 und 8 und auch die Vielfachen von 12. Dies müssen wir solange machen bis wir bei allen drei Reihen eine gemeinsame Zahl finden. Dies ist erst bei der 120 der Fall.

Anzeige:

kgV berechnen mit Primfaktorzerlegung

Eine weitere Möglichkeit das kgV zu finden soll hier gezeigt werden. Diese bezeichnet man als kgV mit Primfaktorzerlegung. Dabei nimmt man die beiden (oder noch mehr) Zahlen und zerlegen diese Zahlen in die Multiplikation aus kleinen Primfaktoren. Gerade beim Ermitteln des kgV von sehr großen Zahlen hilft dieses Verfahren. Um den Rechenweg zu verstehen bleibe ich bei den Beispiel-Rechnungen bei kleinen Zahlen.

Für die Zerlegung sollte man die Teilbarkeitsregeln kennenlernen. Wer die Regeln zur Teilbarkeit noch nicht kennt, kann diese gerne nachlesen. Die Kurzfassung seht ihr jedoch in den Beispielen.

Beispiel 3:

Mit dem kgV zur Primfaktorzerlegung soll das kleinste gemeinsame Vielfache der Zahlen 20 und 24 berechnet werden.

Lösung:

Wir nehmen beide Zahlen und zerlegen diese in die Multiplikation kleiner Primzahlen. Zunächst zerlegen wir die 20 in Primfaktoren

Nun nehmen wir die 24 auseinander und bilden aus dieser Multiplikationen kleiner Primzahlen.

Wir fassen die beiden Primfaktorzerlegungen zusammen:

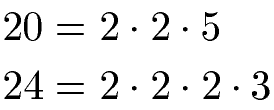
Wir schreiben diese Zerlegung in Potenzen auf.

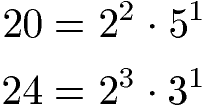
Die Basis - oder besser gesagt die Basen - der Zahlen sind 2, 5 und 3. Diese sehen wir uns nun an und nehmen jeweils die Potenz mit dem höchsten Exponenten. Bei 2² und 2³ hat 2³ den höchsten Exponenten. Bei der Basis 3 gibt es nur 3¹ und bei der Basis 5 nur 5¹.

Man kann dieses kgV noch ausrechnen mit 2³ · 3¹ · 5¹ = 120.

Aufgaben / Übungen zum kgV

Aufgabe 1: Zunächst ein Hinweis: Wer eine Aufgabe nicht mag kann auf "Überspringen" klicken. Ansonsten zur ersten Aufgabe: Wie lautet das kgV von 3 und 5.

• 5
• 15
• 3
• 30

Weiter zur Lösung » Aufgabe überspringen »

Du hast 0 von 6 Aufgaben erfolgreich gelöst.

Anzeigen:

Videos zum kgV

Fragen mit Antworten zum kgV