Rechteck: Eigenschaften und Formeln
Geschrieben von: Dennis RudolphDonnerstag, 15. Februar 2018 um 17:47 Uhr
Was ein Rechteck ist und wie man damit rechnet, lernt ihr hier. Dies sehen wir uns an:
- Eine Erklärung, welche Eigenschaften ein Rechteck hat (Definition).
- Beispiele zum Einsatz der Formeln mit Zahlen und Einheiten.
- Aufgaben / Übungen damit ihr das Rechnen mit dem Rechteck selbst üben könnt.
- Ein Video zum Rechteck.
- Ein Frage- und Antwortbereich zu diesem Thema.
Tipp: Wir sehen uns gleich das Rechteck an. Zum Rechnen damit solltet ihr Wissen was Meter und Zentimeter sind. Falls nicht bitte in Längeneinheiten reinsehen. Die Formeln beinhalten Variablen. Wer noch nicht weiß was das ist sieht bitte in Variablen rein.
Eigenschaften Rechteck und Definition
Wie sieht ein Rechteck aus? Starten wir dafür zunächst mit einem Bild von einem Rechteck:

Für ein Rechteck gilt diese Definition / Eigenschaften:
- Die jeweiligen Gegenseiten sind gleich lang.
- Es gibt vier Ecken.
- Alle Winkel sind 90 Grad.
- Die Summe aller Innenwinkel ist damit 360 Grad.
- Ein Viereck in der Ebene.
- Gegenüberliegende Seiten sind parallel.
- Beide Diagonale sind gleich lang und halbieren einander.
- Es gibt einen Umkreis und zwei Symmetrieachsen.
Wir hatten eben die Merkmale von einem Rechteck. Um jetzt mit einem Rechteck rechnen zu können, schreibt man Variablen (Buchstaben) an die Seiten von einem Rechteck. Dabei bezeichnet man Länge und Breite meistens mit den Variablen a und b.

Rechteck Fläche / Flächeninhalt:
Wie groß ein Rechteck ist, gibt man mit der Fläche bzw. dem Flächeninhalt an. Die Variable in Formeln dafür ist das A. Man berechnet die Fläche, indem man Länge mit Breite multipliziert. Die Formel bzw. Gleichung sieht damit so aus:

Beispiele zur Berechnung der Fläche von einem Rechteck gibt es weiter unten.
Rechteck Umfang Formel / Gleichung:
Der Umfang ist die Strecke, welche man zurücklegen muss, um einmal alle Seiten des Rechtecks abzulaufen. Hätten wir ein Grundstück in Form eines Rechtecks, dann bedeutet der Umfang einmal um dieses Grundstück herumzulaufen. Man erhält den Umfang von einem Rechteck, indem wir alle Seiten addieren. Die Seite a gibt es zwei Mal und die Seite b gibt es zwei Mal. Dies müssen wir addieren:

Beispiele zur Berechnung vom Umfang eines Rechtecks gibt es weiter unten.
Anzeige:
Anzeigen:
Beispiele Rechteck
In diesem Abschnitt sollen einige Beispiele zum Rechteck vorgestellt werden.
Beispiel 1: Rechtecke in der Realität
Nenne einige Objekte, welche die Form von einem Rechteck haben.
Lösung:
Die meisten Vertreter der folgenden Objekte / Gegenstände haben die Form von einem Rechteck:
- Viele Fenster
- Papier
- Bildschirme
- Schreibtische
- Bücher
- Betten
Beispiel 2: Flächeninhalt Rechteck
Ein einfaches Beispiel zum Start: Ein Blatt Papier hat die Form von einem Rechteck. Es ist 30 cm lang und 20 cm breit. Wie groß ist die Fläche?
Lösung:
Wir haben ein Rechteck, daher können wir die Formel A = a · b verwenden. Länge und Breite sind mit 20 cm und 30 cm gegeben. Wir multiplizieren daher die 20 mit 30 und erhalten 600. Und Zentimeter mal Zentimeter ergibt Quadratzentimeter (cm · cm = cm2). Wir erhalten damit eine Fläche von 600 Quadratzentimeter:

Ihr habt dies noch nicht richtig verstanden? Ihr sucht weitere Beispiele (auch komplizierte) und Erklärungen zum Flächeninhalt von einem Rechteck? Dann werft doch noch einen Blick auf unsere Inhalte zu Rechteck Fläche.
Beispiel 3: Umfang Rechteck
Ein einfaches Beispiel zum Start: Wir haben ein Rechteck. Die Länge sei 7 cm und die Breite 9 cm. Wie groß ist der Umfang von diesem Rechteck?
Lösung:
Wir setzen a = 7 cm und b = 9 cm in die Gleichung ein und berechnen damit den Umfang mit der Formel weiter oben zu U = 32 cm.
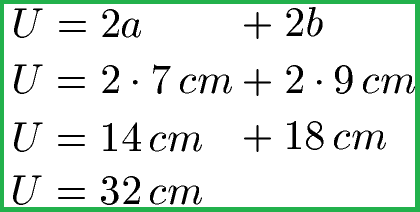
Ihr habt dies noch nicht richtig verstanden? Ihr sucht weitere Beispiele (auch komplizierte) und Erklärungen zum Umfang von einem Rechteck? Dann werft doch noch einen Blick auf unsere Inhalte zu Rechteck Umfang.
Übungen / Aufgaben Rechteck
Anzeigen:Video Rechteck
Beispiele und Erklärungen
Im nächsten Video wird das Rechteck besprochen. Zunächst werden dabei Eigenschaften / Merkmale von einem Rechteck vorgestellt. Im Anschluss geht es um Fläche und Umfang von einem Rechteck.
Nächstes Video »
Fragen mit Antworten zum Rechteck
In diesem Abschnitt sehen wir uns Fragen mit Antworten zum Rechteck an.
F: Ist ein Parallelogramm ein Rechteck?
A: Ja. Ein Rechteck ist ein Spezialfall eines Parallelograms. Ein Parallelogramm ist ein konvexes ebenes Viereck, bei dem gegenüberliegende Seiten parallel sind.
F: Ist ein Quadrat ein Rechteck?
A: Ja. Sind alle Seiten gleich lang bei einem Rechteck wird dieses damit auch zum Quadrat.
F: Wie berechnet man den Umfang mit einer Diagonalen und einer Seite?
A: Ihr habt in diesem Fall ein Dreieck mit einem rechten Winkel innerhalb des Rechtecks. Damit kennt ihr eine Kathete und die Hypotenuse. So etwas kann man mit dem Satz des Pythagoras berechnen. Diesen drückt man mit der Formel a2 + b2 = c2 aus. Mehr dazu im Artikel Satz des Pythagoras.
F: Wie berechnet man Oberfläche und Volumen von einem Rechteck?
A: Die Oberfläche von einem Rechteck berechnet man mit der Formel A = a · b. Wir kennen diese Formel bereits von weiter oben zur Fläche von einem Rechteck. Ein Rechteck selbst hat kein Volumen, denn ein Rechteck ist nur eine Oberfläche. Die die Höhe 0 ist, ist damit automatisch auch das Volumen Null. Erst wenn man das Rechteck erweitert auf ein dreidimensionales Gebilde erhält es ein Volumen.
Neue Artikel
- Raute ▷ Formeln, Eigenschaften und Beispiele
- Sachaufgaben Klasse 5 Mathematik Aufgaben
- Sachaufgaben Mathe: Klasse 5
- Worte in Zahlen Aufgaben (Übungen)
- Worte in Zahlen umwandeln
- Teilerfremdheit (Mathematik)
- Hohlmaße umrechnen
- Hundertertafel Grundschule
- Quersumme berechnen und Teilbarkeit
- Quadratzahlen berechnen (mit Liste)
