Parallelogramm: Eigenschaften und Formeln

Mit dem Parallelogramm beschäftigen wir uns hier. Diese Inhalte sehen wir uns an:

• Eine Erklärung, welche Eigenschaften ein Parallelogramm hat.
• Formeln und Beispiele zum Parallelogramm.
• Aufgaben / Übungen damit ihr dies selbst üben könnt.
• Ein Video zum Parallelogramm.
• Ein Frage- und Antwortbereich zu diesem Thema.

Hinweis: Wir starten mit den Grundlagen zum Parallelogramm, welche schon in der Grundschule behandelt werden. Danach sehen wir uns Formeln zum Rechnen am Parallelogramm an. Falls ihr eure Vorkenntnisse überprüfen möchtet, seht bitte in die Inhalte zum Gleichungen lösen rein.

Parallelogramm: Definition und Eigenschaften

Fangen wir erst einmal mit der Definition von einem Parallelogramm an:

Ein Parallelogramm kann zum Beispiel so aussehen:

Diese Eigenschaften hat ein Parallelogramm:

• Es ist ein Viereck.
• Gegenüberliegende Seiten sind gleich lang (a = c und b = d).
• Gegenüberliegende Winkel sind gleich groß (Alpha und Gamma sowie Beta und Delta).
• Benachbarte Winkel ergänzen sich zu 180 Grad.
• Die Diagonalen halbieren sich gegenseitig.

Die nächste Grafik zeigt noch ein Parallelogramm mit eingezeichneten Diagonalen (blau):

Die Grundlagen zum Parallelogramm werden oftmals bereits in der Grundschule behandelt. Die Berechnungen und Formeln zum Parallelgramm werden ab der 5. Klasse oder spätestens 6. Klasse behandelt.

Anzeige:

Formeln zum Parallelogramm

Die Formeln zum Parallelogramm dienen dazu den Flächeninhalt "A", den Umfang "U", die Höhen "h_a" und "h_b" sowie vier Winkel und die beiden Diagonalen "e" und "f" zu berechnen.

Formel Flächeninhalt Parallelogramm:

Um den Flächeninhalt "A" zu berechnen, wird entweder eine der Seitenlängen ("a" oder "b") benötigt zusammen mit der Höhe auf dieser. Alternativ kann die Fläche über beide Seitenlängen und einen Winkel ausgerechnet werden.

Formel Umfang Parallelogramm:

Um den Umfang "U" zu berechnen, werden die beiden Seitenlängen "a" und "b" benötigt.

Formel Höhen im Parallelogramm:

Um die Höhe auf "a" oder "b" zu berechnen, wird eine Seitenlänge und ein Winkel benötigt.

Winkel-Formeln im Parallelogramm:

Die Summe in einem Viereck beträgt immer 360 Grad. Außerdem zeigen die nächsten Formeln weitere Winkelzusammenhänge beim Parallelogramm.

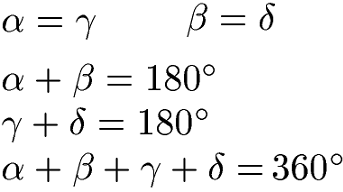
Diagonalen berechnen:

Die Diagonalen werden im Parallelogramm meistens mit "e" und "f" bezeichnet. Sie können mit den folgenden Formeln (greifen auf den Kosinussatz zurück) berechnet werden.

In den nächsten Abschnitten sehen wir uns Beispiele zu den Formeln.

Parallelogramm Fläche (Flächeninhalt) berechnen

Der Flächeninhalt von einem Parallelogramm kann mit mehreren Formeln berechnet werden:

Die Höhen sind über diese Formeln berechenbar:

Beispiel Parallelogramm Fläche:

Wie groß ist der Flächeninhalt dieses Parallelogramms?

Lösung: Wir kennen a = 5 cm und b = 3 cm und den Winkel Alpha mit 30 Grad. Dies nutzen wir und berechnen die Fläche. Wichtig dabei: Den Taschenrechner auf DEG stellen, sonst bekommst du ein komplett falsches Ergebnis.

Anzeigen:

Parallelogramm Umfang berechnen

Der Umfang des Parallelogramms ist die Summe der vier Seiten. Da die gegenüberliegenden Seiten gleich lang sind wird manchmal auch eine zusammenfassende Formel angegeben. Unter dem Strich werden jedoch immer alle vier Seiten zusammen gerechnet.

Beispiel Parallelogramm Umfang berechnen:

Bei einem Parallelogramm sind die Seitenlängen a = 4 cm und b = 3 cm bekannt. Wie groß ist der Umfang von diesem Parallelogramm?

Lösung: Der Umfang berechnet sich als Summe aller vier Längen. In der Aufgabenstellung ist a = 4 cm gegeben, daher ist auch c = 4 cm. Ebenso ist b = 3 cm gegeben, daher ist d = 3 cm. Es folgt die allgemeine Formel für den Umfang von einem Parallelogramm und danach setzen wir ein und rechnen den Umfang aus.

Der Umfang beträgt 14 Zentimeter.

Parallelogramm zeichnen

Ein Parallelogramm hat die Seitenlängen a = 5 cm und d = 3 cm. Der Winkel Alpha sei 30 Grad. Zeichne das Parallelogramm.

Lösung: Mit einem Geodreieck zeichnen wir die Seitenlänge a = 5 cm.

Wir legen das Geodreieck mit der "0" auf die linke untere Ecke der blauen Linie. Wir zeichnen eine kleine Linie unter einem Winkel von 30 Grad. Die rote Linie machen wir dann d = 3 cm lang.

Oben zeichnen wir wieder eine blaue Linie in der Länge von 5 cm an die rote Linie dran. Das Parallelogramm schließen wir wieder mit einer roten Linie von Ecke zu Ecke auf der rechten Seiten.

Zwei benachbarte Winkel ergänzen sich immer zu 180 Grad. Der Alpha-Winkel ist 30 Grad, daher ist Beta 150 Grad. Diese Winkel gibt es auch oben noch einmal. Außerdem schreiben wir die Variablen an die Seiten.

Aufgaben / Übungen Parallelogramm

Aufgabe 1: Bevor wir Rechnen kurz ein paar mehr oder weniger schwere Fragen. Fangen wir einfach an: Wie viele Ecken hat ein Parallelogramm?

• 3
• 5
• 2
• 4

Weiter zur Lösung » Aufgabe überspringen »

Du hast 0 von 5 Aufgaben erfolgreich gelöst.

Video Parallelogramm

Fragen mit Antworten Parallelogramm