Integrationsregeln Mathematik mit Beispiele

Die Integrationsregeln der Mathematik mit Beispielen findet ihr hier. Wer bereits weiß welche Regel gebraucht wird kann sich direkt dorthin begeben. Ansonsten findet ihr ein Stück weiter unten die einzelnen Regeln mit Erklärungen und Beispiele.

Übersicht Integrationsegeln:

• Potenzregel Integration
• Faktorregel Integration
• Summenregel Integration
• Partielle Integration / Produktintegration
• Substitutionsregel

Ihr wisst nicht welche Integrationsregel benötigt wird? Dann werfen wir nun Stück für Stück einen Blick auf die Regeln der Integration. Dabei zeige ich euch welche Funktionen bzw. Gleichungen man damit integriert.

Integrationsregeln mit Beispiele

Die grundlegenden Integrationsregeln werden mit Potenzregel, Faktorregel und Summenregel bezeichnet.

Integrationsregel Potenzregel:

Um Potenzen zu integrieren benötigt man die Potenzregel. Die allgemeine Regel um diese zu integrieren lautet:

Mit dieser Formel kann zum Beispiel diese Potenz integriert werden.

Auch Potenzen in Form von Brüchen können damit integriert werden.

Diese Beispiele ausgerechnet und erklärt erhaltet ihr unter

• Potenzregel Integration

Integrationsregel Faktorregel:

Ein konstanter Faktor kann bei der Integration vor das Integral gezogen werden. Dieser bleibt erhalten. Die allgemeine Formel lautet wie folgt:

Es folgt ein einfaches Beispiel mit der Faktorregel (und zusätzlich der Potenzregel).

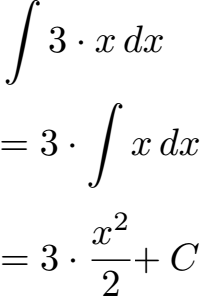
Weitere Beispiele und Erklärungen findet ihr unter:

• Faktorregel Integration

Integrationsregel Summenregel:

Summen und Differenzen dürfen gliedweise integriert werden. Die allgemeine Formel sieht leider sehr unschön aus. Sie besagt jedoch, dass die einzelnen "Teile" der Funktion einzeln integriert werden dürfen wenn ein plus oder minus dazwischen steht.

Anwendung findet dies zum Beispiel bei diesen Aufgaben:

Diese Beispiele vorgerechnet und weitere Erklärungen gibt es unter dem nächsten Link.

• Summenregel Integration

Anzeige:

Integrationsregeln für Produkt, Bruch, E-Funktion, ln und Wurzel

Die partielle Integration wird verwendet um ein Produkt zu integrieren. Die Substitutionsregel - auch Integration durch Substitution genannt - hilft zusätzlich dabei schwierigere Brüche, eine E-Funktionen sowie einen Logarithmus (ln) oder auch eine Wurzel zu integrieren.

Integrationsregel partielle Integration:

Die partielle Integration der Integralrechnung ist eine Regel um einige etwas kompliziertere Funktionen zu integrieren. Die Funktion wird dabei in eine Multiplikation aus zwei Funktionen zerlegt. Die Integration erfolgt durch Einsatz der Formel zur partiellen Integration.

Einige typische Fälle die mit der partiellen Integration integriert werden können:

Weitere Erklärungen und vorgerechnete Beispiele findet ihr unter:

• Partielle Integration / Produktintegration

Integrationsregel Substitutionsregel:

Die Integration durch Substitution - auch Substitutionsregel - ist eine Regel der Mathematik um Funktionen zu integrieren. Dabei versucht man durch Substitution (Ersetzen eines Ausdrucks durch eine andere Variable) eine Funktion zu erzeugen, welche man in einer Integrationstabelle findet.

Die Integration durch Substitution wird zum Beispiel in diesen Fällen verwendet:

Vorgerechnete und erläuterte Beispiele zur Integration durch Substitution (Substitutionsregel) findet ebenfalls bei uns.

• Substitutionsregel / Integration durch Substitution

Integrationsregeln Aufgaben / Übungen

Um die verschiedenen Integrationsregeln anwenden zu lernen haben wir eine Reihe an Übungsaufgaben erstellt. Diese Aufgaben sind unterteilt nach der jeweiligen Integrationsregel. Versucht dabei jeweils die Aufgaben zu lösen ohne mit dem Taschenrechner oder anderen Hilfsmitteln nachzuhelfen.

• Potenzregel Integration Aufgaben / Übungen
• Faktorregel Integration Aufgaben / Übungen
• Summenregel Integration Aufgaben / Übungen
• Partielle Integration Aufgaben / Übungen
• Substitutionsregel Aufgaben / Übungen

Zu jeder Aufgabe gibt es vier Antwortmöglichkeiten von denen nur eine Antwort richtig ist. Die drei anderen Antworten sind falsch. Wer die Antwort nicht weiß kann raten oder direkt zur Lösung springen, welche im Normalfall die Rechnung und eine Erklärung bietet.

Anzeigen:

Video Grundlagen Integration

Fragen mit Antworten zu Integrationsregeln