Faktorregel Integral / Integrieren

Wie man die Faktorregel beim Integrieren anwendet, lernt ihr hier. Dies sehen wir uns an:

• Eine Erklärung, wofür man die Faktorregel bei der Integralrechnung braucht.
• Beispiele für den Einsatz der Faktorregel.
• Aufgaben / Übungen um das Thema selbst zu üben.
• Ein Video zu den Grundlagen der Integralrechnung.
• Ein Frage- und Antwortbereich zu diesem Gebiet.

Tipp: Es ist hilfreich, wenn ihr bereits die Grundlagen der Integration kennt sowie die Potenzregel der Integralrechnung.

Faktorregel beim Integrieren

Es gibt verschiedene Regeln um Funktion zu integrieren. Eine Regel davon wird als Faktorregel bezeichnet.

Bevor wir zu Beispielen kommen erst einmal die allgemeine Formel / Gleichung zur Faktorregel:

Einfaches Beispiele zur Formel:

Integriert werden soll die einfache Funktion f(x) = 3x nach der Variablen x (daher das dx dahinter). Dazu ziehen wir die 3 vor das Zeichen für die Integration und belassen es bei x dx dahinter. Durch die Potenzregel der Integration können wir das x integrieren zu x² : 2. Die 3 davor bleibt stehen und wird mit dem Rest multipliziert. Wir ergänzen eine mögliche Konstante C (das C für eine beliebe Zahl. die beim Ableiten wieder wegfallen würde).

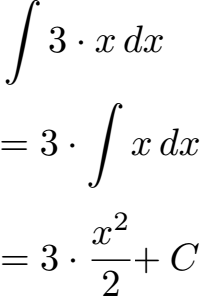
Noch ein Hinweis: Wer die Potenzregel der Integration nicht mehr weiß findet hier noch einmal die Regel:

Anzeige:

Faktorregel Integration Beispiel

Sehen wir uns ein weiteres Beispiel für die Faktorregel der Integralrechnung an.

Beispiel 2: Faktorregel Integration

Wie lautet die Lösung dieser Aufgabe?

Lösung:

Zu Beginn der Lösung noch einmal die Aufgabenstellung und darunter die Potenzregel zum Integrieren der Funktion. Den Bruch - also 2 : 3 - dürfen wir für die Integration vor das Integral ziehen, da es sich um einen konstanten Faktor handelt. Bleibt uns als Potenz x⁴ erhalten. Für die Integration wird die Potenz um 1 erhöht auf 5, welche auch in den Nenner kommt. Im Anschluss müssen wir nur noch ausmultiplizieren.

Soweit die Regel mit Beispielen.

Tipp für die Praxis: Im Prinzip kann man diese Regel auch einfach im Kopf mitbehandeln. Dazu lasst ihr den konstanten Faktor einfach stehen und berechnet den Rest.

Faktorregel Aufgaben / Übungen

Aufgabe 1:

• In welchen Fällen wird die Faktorregel in der Integalrechnung überhaupt eingesetzt?

• Funktion integrieren mit quadratischer Funktion
• Funktion integrieren mit konstantem Faktor
• Integration von einem Bruch mit Variablen in Zähler und Nenner
• Als Ersatz für eine Substitution

Weiter zur Lösung » Aufgabe überspringen »

Du hast 0 von 3 Aufgaben erfolgreich gelöst.

Anzeigen:

Video Integralrechnung

Fragen mit Antworten: Faktorregel Integration