Bestimmtes Integral berechnen / lösen

Was ein bestimmtes Integral ist und wie man es löst, lernt ihr hier. Dies sehen wir uns an:

• Eine Erklärung, was ein bestimmtes Integral ist.
• Beispiele für das Lösen bestimmter Integrale.
• Aufgaben / Übungen um das Thema selbst zu üben.
• Ein Video zur Flächenberechnung mit Integralen.
• Ein Frage- und Antwortbereich zu diesem Gebiet.

Tipp: Ihr solltet bereits wissen was Integrieren überhaupt bedeutet. Wer davon noch keine Ahnung hat wirft bitte erst einmal einen Blick in die Grundlagen der Integration. Auf den Unterschied zwischen bestimmtes Integral und unbestimmtes Integral gehen wir hier noch ein.

Bestimmtes Integral Erklärung

In der Mathematik unterscheidet man zwischen dem unbestimmten Integral und dem bestimmten Integral.

Grundlage unbestimmtes Integral:

Das nächste Beispiel zeigt ein unbestimmtes Integral. So ein Integral hat keine Integrationsgrenzen (es stehen keine Zahlen über oder unter dem Integral). Die Lösung erhält man durch Einsatz der Integrationsregeln (wir rechnen so etwas weiter unten vor). Wir erhalten mit F(x) eine Stammfunktion als Lösung der Aufgabe.

Das Wissen zum unbestimmten Integral hilft auch beim bestimmten Integral.

Bestimmtes Integral:

Der erste Unterschied liegt darin, dass es bei einem bestimmten Integral so genannte Integrationsgrenzen gibt. Man bezeichnet diese als untere Grenze und als obere Grenze. Im nächsten Beispiel sind dies 0 und 2.

Was bedeutet dies? Dazu zeichnen wir uns die Funktion y = 2x einmal in ein Koordinatensystem ein.

Das bestimmte Integral bedeutet, dass man hier eine Fläche berechnen soll. In diesem Fall soll die Fläche unter der Funktion 2x berechnet werden zwischen x = 0 und x = 2 (den Integrationsgrenzen).

Wie man das bestimmte Integral berechnet sehen wir uns im nächsten Abschnitt an.

Anzeige:

Bestimmtes Integral berechnen

Wie kann man ein bestimmtes Integral berechnen? Welche Regeln muss man bei einem bestimmten Integral beachten?

Beispiel 1: Integral berechnen

Wie groß ist die Fläche unter der Funktion y = 2x zwischen x = 0 und x = 2?

Lösung:

Wir wandeln die Aufgabenstellung in eine Aufgabe um. Integriert werden muss nach der Variablen x (daher das dx). Die Integrationsgrenzen sind x = 0 und x = 2, welche wir an das Zeichen für die Integration schreiben.

Um das bestimmte Integral zu lösen, müssen wir die Integrationsregeln der Integralrechnung einsetzen. Es gibt hier mehrere Regeln und alle hier zu erklären würde den Artikel extrem in die Länge ziehen. Daher hier eine Übersicht der Regeln.

• Integrationsregeln
  • Potenzregel Integration
  • Faktorregel Integration
  • Summenregel Integration
  • Partielle Integration / Produktintegration
  • Substitutionsregel

Für unser Beispiel brauchen wir die Potenzregel. Diese wenden wir erst einmal an. Integrieren wir 2x erhalten wir x². Im Gegensatz zum unbestimmten Integral fällt die Konstante + C weg. Die x² schreiben wir diesmal in eckige Klammern und dahinter die Grenzen.

Im Anschluss müssen wir die Grenzen einsetzen. Zunächst setzen wir mit x = 2 die obere Grenze ein. Aus x² wird dadurch 2². Im Anschluss setzen wir die untere Grenze mit x = 0 ein. Aus x² wird 0². Dazwischen setzen wir ein Minuszeichen. Im Prinzip obere Grenze einsetzen minus untere Grenze einsetzen.

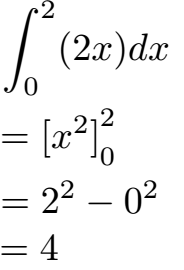
Rechnen wir 2² - 0² aus erhalten wir eine 4 als Ergebnis. Dies ist die Fläche, daher schreibt man manchmal auch 4 FE. Das FE ist die Abkürzung für Flächeneinheiten.

Aufgaben / Übungen bestimmtes Integral

Aufgabe 1:

In diesem Bereich bieten wir euch die Möglichkeit Fragen und Aufgaben zum bestimmten Integral zu üben. Viele Schüler und Studenten scheitern jedoch schon an Begriffen und Wissen zum bestimmten Integral. Daher gibt es hier erst einmal kurz ein paar Fragen zum Thema und danach Aufgaben zum Rechnen. Wer etwas nicht mag kann auf überspringen klicken.

• Woran erkennt man ein bestimmtes Integral (im Vergleich zum unbestimmten Integral)?

• Doppelintegral
• Negative Zahlen
• Es gibt Integrationsgrenzen
• Keine Integrationsgrenzen

Weiter zur Lösung » Aufgabe überspringen »

Du hast 0 von 4 Aufgaben erfolgreich gelöst.

Anzeigen:

Video Integration und Fläche

Fragen mit Antworten zum bestimmten Integral