Erste Nullstelle finden (Polynomdivision)

Wie man eine erste Nullstelle findet (zum Beispiel für die Polynomdivision), lernt ihr hier. Folgende Inhalte werden angeboten:

• Eine Erklärung, wie man eine erste Nullstelle findet.
• Beispiele für kubische Gleichungen.
• Übungen zum Berechnen von Nullstellen.
• Ein Video zur Polynomdivision.
• Ein Frage- und Antwortbereich zu diesem Thema.

Hinweis: Um eine Polynomdivision durchführen zu können, benötigt man eine erste Nullstelle. Wie man diese (in der Schule) findet, lernt ihr hier. Die Polynomdivision sehen wir uns in einem separaten Artikel an. Diesen findet ihr unter Polynomdivision Erklärung.

Erklärung: Erste Nullstelle

Eine Polynomdivision kann nur durchgeführt werden, wenn man bereits eine Nullstelle hat. In der Schule gibt es dazu eigentlich nur ein "Verfahren" um diese zu finden. Dieses lautet: Ausprobieren. Dazu setzen wir in eine Funktion einige Zahlen ein und hoffen darauf eine Nullstelle zu finden.

Beispiel 1: Erste Nullstelle finden

Finde für den folgenden Ausdruck eine erste Nullstelle.

Lösung:

Um eine Nullstelle zu erraten setzt man typischerweise kleine Zahlen ein wie 0, 1, 2, 3, .. oder auch -1, -2, -3... und schaut dann ob das Polynom Null wird. Fangen wir einmal damit an x = 0 einzusetzen.

Das war wohl nichts. Mit 6 = 0 haben wir keine Gleichung. Versuchen wir als nächstes x = 1:

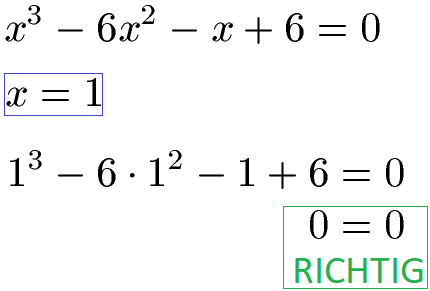
Wir haben bei x = 1 eine Nullstelle. Hinweis: Würden wir nun eine Polynomdivision durchführen um weitere Nullstellen zu finden würde die Aufgabe (x³- 6x² - x + 6) : (x -1) lauten. Diese findet ihr vorgerechnet unter Polynomdivision Erklärung.

Anzeige:

Beispiele erste Nullstelle finden

In diesem Abschnitt sehen wir uns eine kubische Funktion (kubische Gleichung) an.

Beispiel 2: Kubische Funktion erste Nullstelle

Finde für die folgende kubische Funktion die erste Nullstelle. Wo liegt diese?

Lösung:

Wir setzen für x verschiedene Zahlen ein bis wir 0 = 0 erhalten.

Für x = -1 erhalten wir eine korrekte Lösung. Für eine Polynomdivision müsste die Aufgabe (x³ + 8x² + 19x + 12) : (x + 1) berechnet werden.

Aufgaben / Übungen Nullstellen berechnen

Aufgabe 1: Zunächst ein kurzer Hinweis: Wer eine Aufgabe oder Frage nicht mag, kann auf "Überspringen" klicken. Bevor wir Rechnen erst einmal ein paar Fragen zum Einstieg: Welche Eigenschaft haben Nullstellen gemeinsam (in einem normalen x-y-Koordinatensystem wie im Artikel verwendet)?

• x = 0
• z = 0
• y = 0
• a = 0

Weiter zur Lösung » Aufgabe überspringen »

Du hast 0 von 4 Aufgaben erfolgreich gelöst.

Anzeigen:

Video Polynomdivision

Fragen mit Antworten Erste Nullstelle