Ungleichungen lösen

Was eine Ungleichung ist und wie man sie löst, lernt ihr hier. Dies sehen wir uns an:

• Eine Erklärung, was eine Ungleichung ist und mit welchen Regeln man sie löst.
• Beispiele zum Lösen von Ungleichungen (auch mit Fallunterscheidung und Lösungsmenge).
• Aufgaben / Übungen damit ihr dies selbst üben könnt.
• Ein Video zu Ungleichungen.
• Ein Frage- und Antwortbereich zu diesem Thema.

Tipp: Wir sehen uns gleich Ungleichungen an. Es hilft euch enorm dabei zu verstehen, wie man normale Gleichungen löst. Wer einfache Gleichungen noch nicht lösen kann, liest bitte erst einmal unter Gleichung auflösen nach.

Erklärung Ungleichungen lösen

Bei einer Gleichung kommt ein Gleichheitszeichen vor. Das Istgleich wird mit einem "=" dargestellt und kennt man bereits ab der 1. Klasse der Grundschule. Zwei Beispiele:

Vielleicht erinnert sich der eine oder andere noch an Vergleichszeichen für größer und kleiner. Typisch für Ungleichungen in der Schule sind die Zeichen größer, kleiner und manchmal kleiner-gleich und größer-gleich. Eine kleine Übersicht dazu:

Mit diesen Vergleichszeichen kann man Ungleichungen bilden, zum Beispiel:

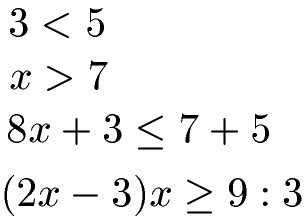
Bei den ersten beiden Ungleichungen gibt es nichts zu rechnen. Bei den unteren beiden Ungleichungen sieht dies anders aus. Daher zunächst einige Regeln zu Ungleichungen und Tipps.

Anzeige:

Beispiele Ungleichungen

In diesem Abschnitt starten wir mit einfachen Beispielen zu Ungleichungen.

Beispiel 1:

Löse die nächste Ungleichung nach x auf und gib die Lösungsmenge an.

Lösung berechnen:

Wir müssen durch Umformungen - auch Äquivalenzumformungen genannt - das x auf eine Seite der Gleichung schaffen und die Zahlen auf die andere Seite. Um dies zu erreichen, subtrahieren wir im ersten Schritt 50. Wir haben danach noch -10 vor dem x. Daher teilen wir durch -10.

Wichtig: Jetzt müssen wir die Regeln von oben beachten, dass bei Multiplikation oder Division mit einer negativen Zahl das Vergleichszeichen umgedreht wird. Seht selbst:

Als Lösung rechnen wir nun aus, dass x = - 15 sein muss oder größer.

Lösungsmenge:

Es gibt viele Möglichkeiten die Lösungsmenge darzustellen. Eine mögliche Lösung lautet:

Was sagt die Lösungsmenge aus? Das L ist die Abkürzung für die Lösungsmenge. Manchmal wird das L auch mit zwei Strichen geschrieben. Danach kommt die eckige Klammer "[", welche zur Zahl geöffnet ist. Diese besagt, dass die -15 noch zur Lösung mit dazugehört. Die umgefallene 8 ist das Zeichen für Unendlich. Per Definition gehört unendlich nicht zum Intervall, daher geht die eckige Klammer mit "[" weg vom Unendlich-Zeichen.

Probe:

Haben wir uns verrechnet? Wer dies prüfen möchte, macht noch eine Probe. Wir setzen unser Ergebnis für x in die Startgleichung ein und schauen, ob wir richtig gerechnet haben. Um rechnen zu können, setzen wir erst einmal die -15 ein.

Mit x = -15 passt es. Wir hatten aber auch berechnet, dass x größer als -15 sein darf. Aufpassen!

Größer als -15 bedeutet damit, dass -14 oder auch -11,7 oder auch +5 größer sind. Die Null (0) ist damit logischerweise auch größer als -15. Würden wir zum Beispiel 0 einsetzen, sähe die Rechnung so aus:

50 ist kleiner als 200. Daher passt das mit der Berechnung unserer Lösungsmenge von weiter oben.

Weitere Typen von Ungleichungen:

Wir hatten eben ein einfaches Beispiel zur Einleitung von Ungleichungen. Dieses Gebiet ist jedoch sehr umfangreich. So gibt es neben den Ungleichungen mit einer Variablen - wie wir diese weiter oben hatten - noch weitere Typen. Alle Arten von Ungleichungen hier ausführlich zu besprechen würde diesen Artikel zu lange werden lassen. Daher eine Übersicht weiterer Ungleichungen.

Sobald die Erklärungen zu den folgenden Typen von Ungleichungen bei uns verfügbar sind, werden diese auch hier verlinkt.

• Lineare Ungleichungen mit zwei Variablen
• Quadratische Ungleichungen
• Bruchungleichungen / Ungleichungen mit Brüchen
• Betragsungleichungen / Ungleichungen mit Betrag
• Lineare Ungleichungssysteme mit einer Variablen
• Lineare Ungleichungssysteme mit zwei Variablen

Ebenfalls in Planung sind diese Inhalte:

• Ungleichungen grafisch lösen
• Ungleichungen Fallunterscheidung

Übungen / Aufgaben Ungleichungen

Aufgabe 1: Viele Schüler und Schülerinnen haben Probleme mit Ungleichungen. Oft scheitert es schon an den Grundlagen. Bevor wir rechnen daher kurz ein paar Fragen zu Ungleichungen. Wer diese nicht mag, kann auf überspringen klicken. Erste Frage: Was bedeutet das Zeichen "<"?

• kleiner
• größer
• größer-gleich
• gleich

Weiter zur Lösung » Aufgabe überspringen »

Du hast 0 von 7 Aufgaben erfolgreich gelöst.

Anzeigen:

Video Ungleichungen

Fragen mit Antworten Ungleichung