Nullstellen berechnen

Wie kann man Nullstellen berechnen? Genau dies sehen wir uns in den nächsten Abschnitten an. Folgende Inhalte werden angeboten:

• Zunächst gibt es Erklärungen, was Nullstellen sind und welche Möglichkeiten es gibt Nullstellen zu berechnen.
• Es werden Beispiele vorgerechnet um die verschiedenen Methoden wie ABC-Formel, PQ-Formel und Polynomdivision zu zeigen.
• Aufgaben und Übungen ermöglichen euch das Berechnen von Nullstellen zu üben.
• Ein Video zum Nullstellen berechnen wird ebenfalls angeboten.
• Ein Frage- und Antwortbereich beantwortet typische Fragen rund um das Auffinden von Nullstellen.

Zunächst erkläre ich ganz kurz, was Nullstellen überhaupt sind. Danach geht es darum welche Typen von Funktionen bzw. Gleichungen es gibt und mit welcher Methode man bei diesen die Nullstellen berechnen kann. Ihr werdet dabei unter Anderem auch die PQ-Formel, die Mitternachtsformel und die Polynomdivision kennenlernen. Wer Probleme mit den Inhalten hat, dem fehlen eventuell ein paar wichtige Vorkenntnisse: In diesem Fall bitte mit den Themen Gleichungen lösen und Funktionen zeichnen befassen.

Erklärung: Nullstellen berechnen

Bevor wir uns das Berechnen von Nullstellen ansehen, sollte zunächst folgende Frage beantwortet werden: Was sind Nullstellen? Nun, die mathematische Beschreibung lautet: Eine Zahl x₀ heißt Nullstelle von f, wenn f(x₀) = 0 ist. Klingt kompliziert, oder? Daher gehen wir mal einen anschaulicheren Weg. Man kann Funktionen oder Gleichungen in ein Koordinatensystem einzeichnen. In der nächsten Grafik wurde diese in blau eingezeichnet. Verfolgt man deren Verlauf, sieht man, dass es eine Stelle gibt, wo diese durch die x-Achse durchläuft. Genau hier haben wir die Nullstelle (in rot eingezeichnet). Und - schaut noch einmal auf die Grafik - genau hier ist y = 0.

Bild 1: Lineare Gleichung (Funktion)

Eine Funktion oder Gleichung kann natürlich mehr als nur eine Nullstellen aufweisen. So zu sehen in der nächsten Grafik, bei der wir eine quadratische Gleichung / Funktion sehen, welche zwei Nullstellen hat (rot eingekreist).

Bild 2: Quadratische Gleichung / Funktion

Anzeige:

Nullstellen: Beispiele und Formeln

Wie kann man Nullstellen berechnen? Um dies zu machen sehen wir uns hier nun zahlreiche Beispiele und entsprechende Formeln an. Der Plan sieht so aus:

Vorgehensweise Nullstellen berechnen:

1. Herausfinden, welchen Typ von Gleichung oder Funktion wir haben.
2. Entsprechende Formel oder Lösungsmethode heraussuchen.
3. Mit dieser Formel oder Methode die Nullstellen berechnen.

Es hilft alles nichts: Wir müssen uns nun ansehen, welche Typen von Gleichungen oder Funktionen es gibt. Damit wir dann entscheiden können, welches Lösungsverfahren wir einsetzen können.

Nullstelle bei linearer Funktion:

Beginnen mit linearen Gleichungen oder linearen Funktionen. Diese haben die Form:

Beispiele für lineare Gleichungen:

Lineare Gleichung Beispiel 1:

Wo liegt die Nullstelle der Gleichung y = x - 2? Lösung: Wir wissen, dass wir zum Auffinden der Nullstelle y = 0 setzen müssen.

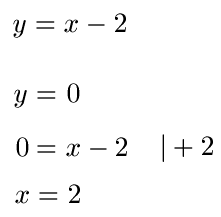
Wir haben bei x = 2 also eine Nullstelle. Und diese Stelle zeichnet sich dadurch aus, dass hier y = 0 ist. Also ist der Punkt der Nullstelle P (2;0).

Lineare Gleichung Beispiel 2:

Wo liegt die Nullstelle bei der Gleichung y = 4x - 4? Lösung: Auch hier setzen wir y = 0 und berechnen dann x.

Bei x = 1 liegt also die Nullstelle. Wir wissen, dass hier auch y = 0 ist. Daher ist der Punkt der Nullstelle P (1;0).

Nullstellen quadratische Gleichung / Funktion:

Kommen wir zum Nullstellen berechnen bei quadratischen Funktionen bzw. quadratischen Gleichungen. Quadratische Gleichungen haben die Form:

Beispiele für quadratische Gleichungen:

:

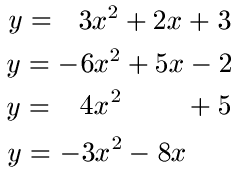Wir wissen nun was quadratische Gleichungen sind. Nur wie löst man diese? Dazu gibt es zwei gängige Verfahren. Zum Einen gibt es die PQ-Formel. Zum Anderen gibt es noch die ABC-Formel, welche manchmal auch Mitternachtsformel genannt wird. Mit der PQ-Formel bzw. ABC-Formel lassen sich quadratische Funktionen (relativ einfach) lösen. Damit ihr seht wie dies geht rechne ich die Aufgabe 3x² + 9x + 5 = - 1 mit beiden Varianten vor.

Quadratische Gleichung Beispiel 1 (mit PQ-Formel):

Bevor wir die PQ-Formel einsetzen können, sollte ihr natürlich erst einmal wissen, wie die PQ-Formel überhaupt aussieht. Um diese einsetzen zu können muss man zunächst dafür sorgen, dass vor x² eine 1 steht und die Gleichung auf die Form mit = 0 gebracht wird. Danach kann man p und q ablesen und einfach einsetzen. Zunächst die Lösungsgleichung, danach das Beispiel.

Wir wollten noch das Beispiel 3x² + 9x + 5 = - 1 lösen um die Nullstellen zu berechnen:

• Wir wissen, dass wir die Gleichung in der Form = 0 brauchen, dazu schaffen wir zunächst die -1 auf der rechten Seite weg.
• Auch brauchen wir vor dem x² eine 1, also 1x² und nicht wie hier 3x². Daher teilen wir durch 3.
• Im Anschluss können wir p und q einfach ablesen und in die Lösungsformel aus der letzten Grafik einsetzen.
• Wir berechnen die Zahlen vor der Wurzel und unter der Wurzel.
• Vor der Wurzel steht ein plus (+) und ein minus(-). Wir berechnen x₁ mit dem plus und x₂ mit dem minus.
• Wir erhalten damit zwei Lösungen. Dies sind die beiden Nullstellen.

Ihr braucht weitere Beispiele und Erklärungen zur PQ-Formel? Dann seht in unseren Artikel PQ-Formel rein.

Quadratische Gleichung Beispiel 2 (mit ABC-Formel):

Die Gleichung - die wir eben mit der PQ-Formel gelöst hatten - soll nun mit der Mitternachtsformel gelöst werden. Zunächst formen wir die Gleichung so um, dass wir = 0 dastehen haben. Wir lesen a, b und c ab und setzen diese in die Lösungsgleichung der ABC-Formel (Mitternachtsformel) ein.

Wie man sehen kann: PQ-Formel und ABC-Formel liefern die gleichen Ergebnisse.

Kubische Funktionen / Funktion 3. Grades, 4. Grades oder höher:

Lineare Funktionen hatten ein x dabei, bei quadratischen Funktionen war die höchste Potenz bei x² erreicht. Und was mache ich nun, wenn ich x³, x⁴ oder gar noch höher habe? Dann brauchen wir die Polynomdivision. Denn mit der Polynomdivision können wir Funktionen 3. Grades, Funktionen 4. Grades oder noch höher lösen.

Polynomdivision setzt sich aus zwei Wörtern zusammen: Polynom und Division. Divisionen kennt ihr schon von der Grundschule, zum Beispiel 6 geteilt durch 2 ist eine Division. Oder ein Bruch mit Zähler und Nenner stellt eine Division dar. Fehlt uns noch Polynom: Ein Polynom ist eine Summe von Vielfachen von Potenzen mit natürlichzahligen Exponenten einer Variablen, die in den meisten Fällen mit x bezeichnet wird.

Beispiele für Polynome:

• 2x² + 5x + 8
• 9x³ + x² + 5x -3
• 18x⁵ + 30x⁴ + 3x

Bei der Polynomdivision teilen wir zwei Polynome durcheinander. Die Vorgehensweise zum Nullstellen berechnen sieht so aus:

• Wir brauchen eine Funktion oder Gleichung, deren Nullstellen wir berechnen wollen.
• Wir brauchen von dieser Funktion bereits eine erste Nullstelle
• Mit dieser ersten Nullstelle kann die Polynomdivision durchgeführt werden.

Beispiel 1 Polynomdivision:

Sehen wir uns ein Beispiel zur Polynomdivision an. Gegeben sei x³ - 6x² - x + 6 = 0. Wo befinden sich die Nullstellen? Lösung: Durch raten erhalten wir eine erste Nullstelle bei x = 1. Daher teilen wir x³ - 6x² - x + 6 durch x - 1. Würde ich bei x - 1 nun x = 1 einsetzen, käme ich auf 0 (Nullstelle). Wir müssen also folgende Aufgabe lösen:

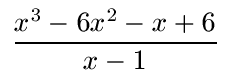
Diese Aufgabe schreiben wir erst einmal anderst hin:

Nun müssen wir anfangen zu rechnen. Dies läuft so ab, dass wir erst einmal eine Division durchführen müssen. Wir berechnen hier zunächst x³ : x. Ein x kürzt sich dabei, sprich x³ : x = x².

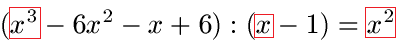
Als nächstes müssen wir multiplizieren. Und zwar berechnen wir x² · (x - 1) = x³ - x². Das Ergebnis schreiben wir unter x³ - 6x².

Nun Subtrahieren wir wie folgt und erhalten -5x².

Wir ziehen nun die -x von oben runter:

Nun beginnt das Spielchen wieder von vorne. Sprich wir müssen nun wieder eine Division durchführen: -5x² : x = -5x

Jetzt multiplizieren wir wieder in die andere Richtung: (-5x) · (x-1) = -5x² + 5x

Und erneut Subtrahieren wir (Siehe roter Kasten im nächsten Bild):

Wir ziehen + 6 runter:

Und nun Dividieren wir wieder: (-6x) : x = -6

Und ein letzes Mal multiplizieren wir: (-6) · (x-1) = -6x + 6

Wenn wir nun Subtrahieren, dann sehen wir, dass 0 herauskommt. Und von oben her (Zähler) gibt es nichts mehr nach unten zu ziehen.

Wir sind damit fertig: Die Polynomdivision ergibt (x³ -6x² - x + 6) : (x-1) = x² -5x -6. Wir wollen jetzt aber die Nullstellen haben (oder habt ihr das nach so einer langen Rechnung bereits vergessen?). Wir haben noch x² -5x -6 übrig. Dies setzen wir gleich Null (= 0). Und dann können wir darauf die PQ-Formel ansetzen. Wer diese noch nicht kennt: Die PQ-Formel wird weiter oben erklärt.

Wenn wir die PQ-Formel nutzen, dann erhalten wir bei x₁ = 6 und bei x₂ = -1 Nullstellen. Vorher hatten wir eine Polynomdivision durchgeführt. Bei dieser hatten wir ganz am Anfang gesagt, dass bei x = 1 noch eine Nullstelle liegt. Wir haben also bei x₃ = 1 noch eine dritte Nullstelle.

Nullstellen Aufgaben / Übungen

Aufgabe 1: Zunächst ein kurzer Hinweis: Wer eine Aufgabe oder Frage nicht mag, kann auf "Überspringen" klicken. Bevor wir Rechnen erst einmal ein paar Fragen zum Einstieg: Welche Eigenschaft haben Nullstellen gemeinsam (in einem normalen x-y-Koordinatensystem wie im Artikel verwendet)?

• x = 0
• y = 0
• a = 0
• z = 0

Weiter zur Lösung » Aufgabe überspringen »

Du hast 0 von 4 Aufgaben erfolgreich gelöst.

Anzeigen:

Nullstellen berechnen Video

Berechnung Nullstellen: Fragen und Antworten