Polynomdivision: Erklärung und Beispiele

Mit der Polynomdivision befassen wir uns in diesem Artikel. Folgende Inhalte werden angeboten:

• Eine Erklärung, was die Polynomdivision ist, wozu man sie braucht und wie sie funktioniert.
• Beispiele zur Polynomdivision werden vorgerechnet.
• Aufgaben / Übungen zur Polynomdivision, damit ihr selbst üben könnt.
• Videos zu diesem Thema, bei denen auch Beispiele vorgerechnet werden.
• Ein Frage- und Antwortbereich zur Division von Polynomen.

Wir sehen uns gleich die Polynomdivision an. Dabei geht es vor allem darum die Berechnung durchzuführen. Wem dies noch nicht langt, der kann gerne auch noch einen Blick in den Artikel Nullstellen berechnen werfen. Dort wird das Thema Polynomdivision gemeinsam mit der PQ-Formel und Nullstellen erneut aufgegriffen.

Polynomdivision Erklärung

Das Wort Polynomdivision setzt sich aus zwei Wörtern zusammen: Polynom und Division.

• Division: Divisionen sollten euch eigentlich schon aus der Grundschule bekannt sein. 8 geteilt durch 2 ist eine Division, also eine Geteiltaufgabe. Ein Bruch mit Zähler und Nenner stellt eine Division dar.
• Polynom: Unter einem Polynom versteht man eine Summe von Vielfachen von Potenzen mit natürlichzahligen Exponenten einer Variablen, welche man oft mit x bezeichnet.

Polynome Beispiele:

• 3x² + 8x + 9
• 91x³ + x² + 4x -5
• 19x⁵ + 20x⁴ + 2x

Bei der Polynomdivision dividieren wir zwei Polynome durcheinander. Die Polynomdivision wird benutzt um Nullstellen zu berechnen. Das sind die Stellen, an denen der Verlauf der Kurve die x-Achse schneidet, also y = 0 ist. Die nächste Grafik zeigt zwei Nullstellen bei einer quadratischen Gleichung, welche in rot markiert sind.

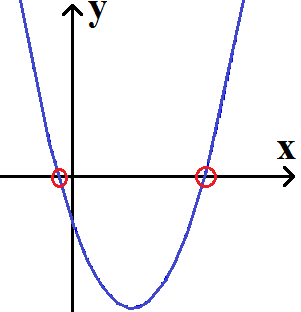
Die Polynomdivision setzt man ab Funktionen 3. Grades ein, also bei Funktionen / Gleichungen mit x³, x⁴ oder noch höher. Dies könnte so aussehen:

• x³ + 3x² + 4x + 1 = 0
• x⁴ + 6x² -8x - 2 = 0
• x⁵ - 3x⁴ + 2x³ + 4x² + 8x - 10 = 0

Anzeige:

Beispiele Polynomdivision

Am besten sehen wir uns die Polynomdivision Schritt für Schritt bei einem Beispiel an. Nehmen wir einmal das Polynom x³ - 6x² - x + 6 und Teilen dies durch das Polynom x - 1. Damit sieht die Aufgabe so aus:

Wir ändern erst einmal die Schreibweise:

Das Rechnen läuft so ab, dass wir erst einmal Dividieren müssen. Wir rechnen hier zunächst x³ : x. Ein x kürzt sich dabei raus, sprich x³ : x = x².

Eine Multiplikation steht nun an. Als nächstes rechnen wir x² · (x - 1) = x³ - x². Dies schreiben wir unter x³ - 6x².

Dies ziehen wir ab und erhalten -5x².

Das -x ziehen wir nun runter:

Jetzt geht alles wieder von vorne los. Also Division: -5x² : x = -5x

Nun wieder eine Multiplikation in die andere Richtung: (-5x) · (x-1) = -5x² + 5x

Es erfolgt wieder eine Subtraktion:

Wir ziehen + 6 runter um weiterrechnen zu können:

Nun folgt wieder eine Division: (-6x) : x = -6

Fehlt uns noch eine letzte Multiplikation: (-6) · (x-1) = -6x + 6

Wenn wir nun Subtrahieren, bekommen wir eine 0 raus. Und von oben her (Zähler) gibt es nichts mehr nach unten zu ziehen. Die komplette Polynomdivision sieht damit wie folgt aus:

Wir sind mit der Polynomdivision nun fertig. Das Ergebnis der Division ist also x² -5x -6.

Polynomdivision Aufgaben / Übungen

Aufgabe 1: In diesem Bereich findet ihr noch Aufgaben und Fragen zur Polynomdivision. Wer eine Frage oder Aufgabe nicht mag, der kann auf "Überspringen" klicken. Zur ersten Übung: Was kann man mit der Polynomdivision rausfinden?

• Hypotenuse
• Kathete
• x-Achse
• Nullstellen

Weiter zur Lösung » Aufgabe überspringen »

Du hast 0 von 2 Aufgaben erfolgreich gelöst.

Anzeigen:

Videos zur Polynomdivision

Fragen und Antworten zur Polynomdivision