Betragsgleichungen

Wie man Betragsgleichungen mit einem oder mehreren Beträgen löst, lernt ihr hier. Dies sehen wir uns an:

• Eine Erklärung was Betragsgleichungen sind und wie man sie berechnet.
• Beispiele wie man Gleichungen mit einem oder mehreren Beträgen löst.
• Aufgaben / Übungen damit ihr dies selbst üben könnt.
• Ein Video zu Betragsgleichungen.
• Ein Frage- und Antwortbereich zu diesem Thema.

Tipp: Betragsgleichungen sind ein Mix aus Gleichungen und Beträge. Wer Gleichungen und Beträge nicht kennt, sieht bitte zunächst in lineare Gleichungen lösen und Betrag Mathematik rein.

Betragsgleichung mit einem Betrag

Eine Betragsgleichung ist eine Gleichung, in der eine oder mehrere Beträge vorkommen. Um solche Aufgaben lösen zu können, muss man sich zunächst klar machen, was "Betrag" überhaupt bedeutet. Dies kann man sehr einfach an einem Beispiel zeigen. So ist der Betrag von +5 und von -5 stets +5.

Beispiel 1: Betragsgleichung mit einem Betrag

Sehen wir uns zum Einstieg eine Betragsgleichung mit einem Betrag an. Wie lautet die Lösung dieser Aufgabe?

Lösung:

Es gibt zwei Möglichkeiten: Entweder ist 3x + 2 = 4 oder 3x + 2 = -4. Denn wenn ich den Betrag von 4 nehme ist dies 4. Jedoch ist auch der Betrag von -4 gleich 4. Ich schreibe dies einmal in rot dran.

Wie löst man dies nun? Dazu gibt es verschiedene Möglichkeiten. Eine Möglichkeit besteht darin, dass man aus der Formulierung von eben einfach zwei Gleichungen macht. Diese bedeutet, dass 3x + 2 entweder +4 sein muss oder 3x + 2 ist -4. Dies sind zwei Gleichungen, die wir einfach lösen können.

Das x kann entweder -2 sein oder +0,66666....

Anzeige:

Betragsgleichung mit mehreren Beträgen

In diesem Abschnitt sehen wir uns Betragsgleichungen mit mehreren Beträgen an. Dabei geht es sowohl um "einfache" Betragsgleichungen ohne Variablen in den Beträgen also auch im Anschluss mit Variablen.

Beispiel 2: Gleichung mit 2 Beträgen

Eine Betragsgleichung mit zwei Beträgen soll gelöst werden. Dabei arbeiten wir von innen nach außen und berechnen zunächst 24 - 69 = -45. Der Betrag davon ist +45, wobei das Minuszeichen vor dem Betragsstrich erhalten bleibt. Wir berechnen noch 24 - 45 = -21. Der Betrag davon ist +21.

Wir erhalten x = 21 als Lösung.

Beispiel 3: Betragsgleichung mit mehreren Beträgen

In diesem Beispiel gibt es links und rechts vom Istgleich-Zeichen einen Betrag. Wie groß ist x?

Lösung:

Zunächst vereinfachen wir die rechte Seite der Gleichung.

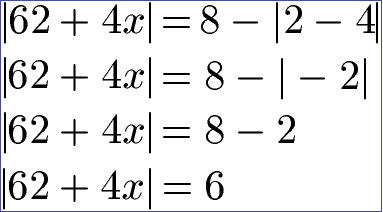
Im Anschluss müssen wir eine Fallunterscheidung durchführen. Dazu lassen wir zunächst beim Betrag die Betragszeichen weg und berechnen im Anschluss - wie man das von einfachen Gleichungen her kennt - das x. Um dies zu erreichen, bringen wir die 4x auf die rechte Seite und alle Zahlen auf die linke Seite.

Wir erhalten x = -14 als erste Lösung. Wir haben jedoch noch einen zweiten Fall: Dazu nehmen wir das was zwischen den Betragsstrichen steht und setzen davor ein Minus und den Inhalt in Klammern. Vor der Klammer steht nun ein Minuszeichen. Dies sorgt dafür, dass beim Auflösen der Klammer sich alle Vorzeichen in der Klammer umdrehen. Im Anschluss lösen wir erneut nach x auf.

Für den zweiten Fall erhalten wir x = -17 als Lösung. Dies bedeutet, dass die Betragsgleichung sowohl mit x = -14 als auch mit x = -17 korrekt gelöst wird.

Aufgaben / Übungen Betragsgleichungen

Aufgabe 1: Bevor wir Gleichungen mit Beträgen rechnen zunächst ein paar ganz einfache Grundlagen. Starten wir kurz mit dem Betrag von Zahlen, damit ihr das erst einmal drauf habt. Wem das zu langweilig ist, der kann natürlich auf "Weiter" klicken. Oder zeigen, dass er / sie es wirklich kann!

Wie lautet der Betrag von -5?

• -5
• -10
• 5
• 10

Weiter zur Lösung » Aufgabe überspringen »

Du hast 0 von 5 Aufgaben erfolgreich gelöst.

Anzeigen:

Video Betragsgleichungen