Gauß-Algorithmus bzw. Gauß-Verfahren

Wie man das Gauß-Verfahren (auch Gauß-Algorithmus oder Gauß Eliminationsverfahren genannt) verwendet, lernt ihr hier. Dies sehen wir uns an:

• Eine Erklärung wie man das Gauß-Verfahren bzw. den Gauß-Algorithmus nutzt.
• Beispiele wie man damit Gleichungssysteme löst.
• Aufgaben / Übungen damit ihr dies selbst üben könnt.
• Ein Video zu linearen Gleichungssystemen.
• Ein Frage- und Antwortbereich zum Gauß Eliminationsverfahren.

Tipp: Das Gauß-Verfahren ist eine Möglichkeit ein lineares Gleichungssystem zu lösen. Weitere Verfahren lernt ihr in unserem Hauptartikel unter lineare Gleichungssysteme lösen.

Erklärung Gauß Eliminationsverfahren

In der Mathematik werden immer wieder Gleichungen gelöst. In einigen Fällen kommt es vor, dass man mehrere Gleichungen mit mehreren Variablen (x, y, z oder andere) hat. Diese Gleichungen müssen gemeinsamen gelöst werden. So etwas nennt man dann das Lösen eines (linearen) Gleichungssystems.

Eine Möglichkeit ein Gleichungssystem zu lösen nennt man Gauß-Verfahren. Andere Namen dafür sind Gauß-Algorithmus oder Gauß Eliminationsverfahren. Wir halten also fest:

Das Ziel mit dem Gauß-Verfahren besteht darin, dass ein Gleichungssystem entsteht, bei dem in der ersten Zeile alle Variablen enthalten sind und in jeder weiteren Zeile darunter je eine Variable beseitigt wurde. Die Vorgehensweise sieht wie folgt aus:

1. Alle Terme mit Variablen auf eine Seite der Gleichung schaffen und nur die Zahlen auf die andere Seite.
2. Bei allen Gleichungen sollen die selben Variablen untereinander stehen.
3. Durch Multiplikation oder Division bei allen Gleichungen gleiche Faktoren erzeugen (Vorzeichen verschieden ist aber OK).
4. Durch Addition oder Subtraktion der Gleichungen eine Variable raus werfen.
5. Dies solange wiederholen, bis nur eine Variable übrig bleibt und diese berechnen.
6. Rückwärts einsetzen um alle verbleibenden Variablen zu berechnen.

Hinweis: Man kann beim Gauß-Verfahren viele Schritte sehr kurz zusammenfassen. Jedoch haben viele Anfänger dadurch Probleme die Rechenschritte zu verstehen. Jeder muss für sich entscheiden, wie viele Schritte zum Lösen nötig sind.

Zum besseren Verständnis sehen wir uns im nächsten Abschnitt ein Beispiel an, welches etwas ausführlicher berechnet und erklärt wird.

Anzeige:

Beispiel Gaußsches Eliminationsverfahren einfach erklärt

Sehen wir uns das Gaußsche Eliminationsverfahren einmal näher an.

Beispiel 1: 3 Gleichungen mit 3 Unbekannten

Wir haben ein lineares Gleichungssystem mit drei Gleichungen und drei Unbekannten. Dieses soll mit dem Gaußschen Eliminationsverfahren gelöst werden. Wie groß sind x, y und z? Gib die Lösungsmenge an.

Lösung:

Zunächst bringen wir alle Variablen auf die linke Seite der Gleichung und die reinen Zahlen auf die rechte Seite der Gleichung. Dabei sollen die Terme mit x, y und z untereinander stehen.

Zunächst wollen wir x eliminieren. Durch Multiplikation oder Division bei allen Gleichungen sollen gleiche Faktoren bei allen Gleichungen erzeugt werden. Dies erreichen wir am einfachsten, indem wir 6x bei jeder Gleichung erzeugen. Daher multiplizieren wir die erste Gleichung mit 6, die zweite Gleichung mit 2 und die dritte Gleichung multiplizieren wir mit 3.

Nun subtrahieren wir:

• Wir nehmen die oberste Gleichung und subtrahieren davon die mittlere Gleichung. Vorne erhalten wir 6x - 6x = 0. Danach 6y - (-2y) = 8y und -12z - 2z = -14z. Auf der rechten Seite 42 - 4 = 38.
• Wir nehmen die oberste Gleichung und subtrahieren davon die unterste Gleichung. Vorne erhalten wir 6x - 6x = 0. Danach 6y - 9y = -3y. Außerdem -12z -15z = -27z. Auf der rechten Seite 42 - 24 = 18.

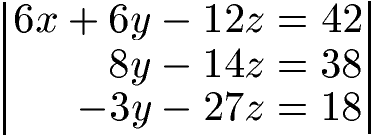
Mit 8y -14z = 38 und -3y - 27z = 18 haben wir noch zwei Gleichungen mit zwei Unbekannten. Als nächstes werfen wir y raus. Um dies zu erreichen multiplizieren wir die mittlere Gleichung mit 3 und die unterste Gleichung mit 8.

Wir addieren nun: Die mittlere Gleichung plus die unterste Gleichung. Wir erhalten 24y + (-24y) = 0. Außerdem -42z + (-216z) = -258z. Auf der rechten Seite der Gleichung erhalten wir 114 + 144 = 258.

Durch -258z = 258 erhalten wir z = -1 als Lösung. Dies setzen wir in die mittlere Gleichung 24y -42z = 114 ein und berechnen damit y = 3.

Mit y und z gehen wir in eine Gleichung mit allen Variablen und rechnen noch x aus.

Wir haben die Lösung berechnet. Wir erhalten x = 2, y = 3 und z = -1.

Aufgaben / Übungen Gleichungssysteme

Aufgabe 1: Wie groß sind x und y im nächsten Gleichungssystem?

• x = 2 und y = 4
• x = 3 und y = 3
• x = 1 und y = 5
• x = 4 und y = 2

Weiter zur Lösung » Aufgabe überspringen »

Du hast 0 von 7 Aufgaben erfolgreich gelöst.

Anzeigen:

Video Gauß-Verfahren / Gauß-Algorithmus

Nächstes Video »

Fragen mit Antworten zum Gauß-Verfahren