Binomische Formeln rückwärts: Faktorisieren / Ausklammern

Wie man die Binomischen Formeln rückwärts nutzt, lernt ihr hier. Dies sehen wir uns an:

• Eine Erklärung was das Ausklammern (Faktorisieren) mit Binomischen Formeln ist.
• Beispiele für alle drei Binomischen Formeln.
• Aufgaben / Übungen damit ihr dies selbst üben könnt.
• Ein Video zum Dreisatz.
• Ein Frage- und Antwortbereich zu diesem Thema.

Tipp: Wir sehen uns gleich an, wie man die Binomischen Formeln rückwärts anwendet. Es hilft dabei sehr, wenn ihr bereits wisst, was die Binomischen Formeln sind. Wer davon noch keine Ahnung hat, sieht bitte in Binomische Formeln rein.

Erklärung Binomische Formeln rückwärts

Sehen wir uns erst einmal an, was man unter den Binomischen Formeln rückwärts überhaupt versteht.

In den meisten Fällen nutzt man die Binomischen Formeln dazu, um bestimmte Klammern aufzulösen. Es geht jedoch auch in die andere Richtung: Klammern erzeugen mit den Binomischen Formeln. Wie dies geht, sehen wir uns nun durch einige Beispiele an. Dazu erst einmal ein Beispiel für jede der drei Gleichungen und im Anschluss noch eine Aufgabe, bei der es nicht klappt.

Beispiel 1: Erste Binomische Formel

Wenn wir drei Terme haben, davon zwei Quadrate und dazwischen zwei Pluszeichen, dann können wir versuchen die 1. Binomische Formeln zu verwenden. Auf diese Gleichung soll sie angewendet werden.

Lösung:

Wir schreiben zunächst die 1. Binomische Formel in die oberste Zeile und darunter unsere Beispielaufgabe. Wir bilden die Gleichungen wie farbig umrahmt. Wir nehmen uns das erste Quadrat mit a² = 4p² und ziehen die Wurzel und erhalten a = 2p. Danach nehmen wir uns das letzte Quadrat b² = 25q² und ziehen dir Wurzel um b = 5q zu erhalten.

Wir kennen damit a und b. Wir bilden noch die Gleichung 2ab = 20pq, welche blau umrahmt ist. Hier setzen wir a und b ein und erhalten 20pq = 20pq. Das bedeutet, dass wir hier korrekt die 1. Binomische Formel verwenden dürfen. Am Ende nehmen wir in die Gleichung der 1. Binomischen Formel und setzen für a = 2p und b = 5q ein.

Anzeige:

Binomische Formeln Faktorisieren / Ausklammern

In diesem Abschnitt sehen wir uns drei weitere Beispiele zum Faktorisieren / Ausklammern mit Binomischen Formeln an.

Beispiel 2: Zweite Binomische Formel

Wenn wir drei Terme haben, davon zwei Quadrate und dazwischen ein Pluszeichen und vorm nichtquadratischen Term ein minus, dann können wir versuchen die 2. Binomische Formeln zu verwenden. Auf diese Gleichung soll sie angewendet werden.

Lösung:

Wir bilden zunächst wieder mit den Quadraten Gleichungen. Bei a² = 0,25d² ziehen wir die Wurzel und erhalten a = 0,5d. Dies machen wir auch mit b² = 2,25e² und erhalten b = 1,5e. Wir kennen damit a und b. Wir bilden eine weitere Gleichung mit 2ab = 1,5de und setzen hier a und b ein. Die Gleichung stimmt mit 1,5de = 1,5de. In die Ausgangsgleichung - also die zweite Binomische Formel - setzen wir a und b ein.

Beispiel 3: Dritte Binomische Formel

Wir haben zwei Terme mit einem Quadrat und dazwischen ein Minuszeichen. In diesem Fall können wir die 3. Binomische Formel probieren. Die Aufgabe dafür lautet:

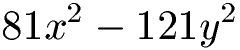
Lösung

Wir bilden zwei Gleichungen mit a² = 81x² und b² = 121y². Aus beidem können wir die Wurzel ziehen. Damit ermitteln wir a und b, was wir in die normale 3. Binomische Formel einsetzen können.

Beispiel 4: Binomische Formel funktioniert nicht

Wir hatten drei Beispiele, die funktioniert hatten. Im vierten Beispiel soll einmal gezeigt werden, dass dies nicht immer der Fall ist. Auf dieses Beispiel soll die Binomischen Formeln rückwärts angewendet werden.

Lösung:

Wir haben drei Terme mit zwei Quadraten und jeweils ein Pluszeichen dazwischen. Daher probieren wir die 1. Binomische Formel. Wir bilden erneut die Gleichungen, siehe die farbigen Markierungen und ziehen die Wurzel. Damit berechnen wir a und b. In blau eingerahmt bilden wir eine weitere Gleichung und setzen a und b ein. Hier sieht man, dass die Gleichung nicht stimmt. Daran sieh man, dass die Binomischen Formeln nicht benutzt werden dürfen.

Aufgaben / Übungen Binomische Formeln rückwärts

Aufgabe 1: Wende die Binomischen Formeln rückwärts auf den folgenden Term an. Wie lautet die Lösung?

4x² + 12x + 9

• (4x + 2)²
• Keine Lösung
• (x + 3)²
• (2x + 3)²

Weiter zur Lösung » Aufgabe überspringen »

Du hast 0 von 6 Aufgaben erfolgreich gelöst.

Anzeigen:

Video Binomische Formeln rückwärts

Fragen mit Antworten Binomische Formeln Faktorisieren / Ausklammern