Lineare Gleichung / Funktion zeichnen und Steigung

Wie man eine lineare Gleichung bzw. Funktion zeichnet und die Steigung berechnet, lernt ihr hier. Dies sehen wir uns an:

• Eine Erklärung wie man eine lineare Funktion / Gleichung zeichnet.
• Beispiele für das Zeichnen im Koordinatensystem und Berechnen der Steigung.
• Aufgaben / Übungen damit ihr dies selbst üben könnt.
• Ein Video zu linearen Gleichungen.
• Ein Frage- und Antwortbereich zu diesem Thema.

Tipp: Wir sehen uns gleich an wie man lineare Funktionen zeichnet. Hilfreich beim verstehen ist es, wenn ihr bereits wisst, was eine Gleichung ist. Wer davon noch keine Ahnung hat sieht bitte in Gleichungen auflösen rein.

Erklärung: Lineare Gleichung zeichnen

Im ersten Beispiel soll eine lineare Gleichung gezeichnet werden. Wir nehmen dazu das Beispiel y = 2x + 1. Um die Funktion zu zeichnen, setzen wir für x verschiedene Zahlen ein, um eine Wertetabelle zu berechnen.

Aus der Wertetabelle können wir direkt ablesen wie sich x- und y- Wert zueinander verhalten. Wir können damit direkt ablesen wo sich der Punkt befindet. Um die Wertetabelle zu berechnen, nehmen wir x = 0, x = 1, x = 2, x = -1 und x = -2. Setzen wir diese Zahlen in die Gleichung ein, können wir damit y berechnen. Die y-Werte sind dabei rot umrahmt und die x-Werte blau.

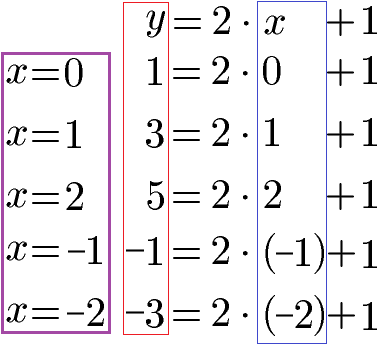
Wir legen eine Tabelle an und vervollständigen diese mit den Zahlen für x und y aus der letzten Berechnung.

Die Wertetabelle zeigt nun Punkte mit x und y. Diese Punkte kann man nun verwenden und in ein Koordinatensystem einzeichnen. Das bedeutet, dass man zum Beispiel bei x = 0 und y = 1 eine Markierung macht. Die nächste Markierung wäre bei x = 1 und y = 3. So kann man dies für einige Punkte machen. Kleiner Tipp: Eigentlich langt bei einer linearen Funktion oder Geraden zwei Punkte. Warum sieht man in der nächsten Grafik: Es handelt sich einfach um eine Gerade.

Anzeige:

Beispiel: Steigung lineare Funktion

Wer einen Berg hochläuft weiß sehr schnell was Steigung bedeutet. Je höher die Steigung, desto anstrengender ist es, auf den Berg zu laufen. Auch in der Mathematik kann man eine Steigung berechnen. Bei einer linearen Funktion bzw. linearen Gleichung ist dies recht einfach zu ermitteln.

Beispiel: Steigung berechnen

Wir nehmen das Beispiel 1 aus dem letzten Abschnitt. Am Ende hatten wir die lineare Funktion y = 2x + 1 in ein Koordinatensystem gezeichnet. Die Steigung können wir ermitteln, indem wir daran ein Steigungsdreieck anzeichnen und dieses auswerten. Daher nehmen wir uns die letzte Grafik und zeichnen uns an einer beliebigen Stelle an Steigungsdreieck ein.

Sowohl auf der x-Achse als auch auf der y-Achse zählen wir nun wie viele Einheiten dies jeweils sind. Auf der x-Achse geht es dabei von -1 auf +1, also sind es 2 Einheiten. Auf der y-Achse gehen wir von -1 auf +3. Dies sind 4 Einheiten.

Die Steigung berechnet man als Quotient von y-Achse und x-Achse. Die Steigung wird mit "m" bezeichnet. Für unser Beispiel gilt:

Dies war die einfache Art der Berechnung. Meistens wird die Berechnung etwas komplizierter dargestellt. Allgemein wird die Formel für die Steigung so angegeben:

Für unser Beispiel von eben lesen wir die x-Werte und y-Werte ab. Werft einen Blick auf das Steigungsdreieck und wo dieses an der linearen Funktion ankommt. Wir erhalten damit:

Aufgaben / Übungen Funktion bzw. Gleichung zeichnen

Aufgabe 1: Wie viele Punkte muss man mindestens berechnen um eine lineare Funktion / Gleichung zu zeichnen?

• Mindestens 4 Punkte
• Mindestens 5 Punkte
• Mindestens 3 Punkte
• Mindestens 2 Punkte

Weiter zur Lösung » Aufgabe überspringen »

Du hast 0 von 4 Aufgaben erfolgreich gelöst.

Anzeigen:

Video Lineare Funktion

Fragen mit Antworten: Zeichnen und Steigung