Äquivalenzumformung

Was die Äquivalenzumformung ist und wozu man diese braucht, lernt ihr hier. Diese Inhalte sehen wir uns an:

• Eine Erklärung, wofür man die Äquivalenzumformung braucht.
• Beispiele zum Anwenden dieser Art der Umformung.
• Aufgaben / Übungen damit ihr dies selbst üben könnt.
• Ein Video zum Lösen von Gleichungen.
• Ein Frage- und Antwortbereich zu diesem Thema.

Hinweis: Wer die Äquivalenzumformung nicht versteht, der hat vielleicht ein paar Probleme mit seinen Vorkenntnissen. In diesem Fall bitte einmal in die Grundrechenarten (Addition, Subtraktion, Multiplikation und Division) reinsehen sowie in Variablen.

Erklärung: Äquivalenzumformung

Was versteht man unter der Äquivalenzumformung?

Beispiel 1: Äquivalenzumformung einfache Gleichung:

Die Gleichung 7 + x = 10 soll durch Äquivalenzumformung nach x aufgelöst werden.

Lösung:

Dies bedeutet, dass wir die Gleichung so verändern müssen, dass x auf einer Seite steht und die Zahlen auf der anderen Seite. In diesem Beispiel ist es recht einfach. Wir haben auf der linken Seite eine Addition von 7 + x stehen. Die Umkehrung der Addition ist die Subtraktion. Um die +7 auf der linken Seite weg zu bekommen, muss -7 auf beiden Seiten der Gleichung gerechnet werden.

Dies eben war eine Äquivalenzumformung. Wir haben die Gleichung verändert, aber der Wert für x - den wir gleich berechnen - ändert sich nicht. Wir rechnen nun links und rechts aus. Auf der linken Seite fallen mit 7 - 7 die beiden Zahlen raus und es bleibt nur x übrig. Auf der rechten Seite erhalten wir 10 - 7 = 3.

Wir berechnen die Lösung zu x = 3. Wir überprüfen zur Sicherheit die Berechnung: Dazu setzen wir die 3 in die Ausgangsgleichung ein und sehen, dass wir mit 10 = 10 eine richtig gelöste Gleichung haben.

Weitere Beispiele wie man einfache Gleichungen löst - auch mit Subtraktion, Multiplikation oder Division - findet ihr unter Gleichung auflösen / umstellen und auch unter lineare Gleichung lösen.

Äquivalenzumformung: Klammer und Brüche

Gleichungen können auch Klammern und Brüche enthalten. Diese müssen bei der Äquivalenzumformung auch beachtet werden. Eine mögliche Gleichung mit Klammer kann zum Beispiel so aussehen:

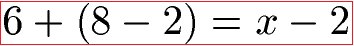
Wie man so etwas löst erfahrt ihr unter Gleichungen mit Klammer.

Gleichungen können auch Brüche enthalten. Man bezeichnet diese dann auch als Bruchgleichungen. Auch hier müssen Regeln der Mathematik und die Äquivalenzumformung beachtet werden, um die Aufgaben zu lösen. Ein mögliches Beispiel:

Wie man Bruchgleichungen löst lernt ihr unter Gleichungen mit Brüche.

Äquivalenzumformungen Beispiele für Ungleichungen

Nicht nur Gleichungen werden mit Äquivalenzumformungen gelöst, sondern auch Ungleichungen. Sehen wir uns dazu ein Beispiel an:

Beispiel 2: Äquivalenzumformung Ungleichungen

Die folgende Ungleichung soll durch Äquivalenzumformungen nach x aufgelöst werden.

Lösung:

Wir müssen durch Umformungen das x auf eine Seite der Ungleichung schaffen und die Zahlen auf die andere Seite. Aus diesem Grund subtrahieren wir im ersten Schritt 50. Wir haben danach noch die Zahl -10 vor dem x. Daher teilen wir durch -10.

Wichtig: Jetzt müssen wir die Mathematik-Regel beachten, dass bei Multiplikation oder Division mit einer negativen Zahl das Vergleichszeichen umgedreht wird:

Als Lösung der Ungleichung rechnen wir nun aus, dass x = - 15 sein muss oder größer.

Weitere Beispiele zum Lösen von Ungleichungen findet ihr unter Ungleichungen lösen.

Äquivalenzumformungen Wurzel und Quadrieren:

Es gibt noch weitere Möglichkeiten für die Äquivalenzumformungen. Darunter fallen zum Beispiel das Ziehen der Wurzel oder das Quadrieren. Dazu haben wir aktuell noch keine Inhalte online. Sobald verfügbar, werden diese hier verlinkt.

Aufgaben / Übungen Äquivalenzumformungen

Wir haben die Aufgaben bzw. Übungen zu diesem Gebiet in verschiedene Bereiche unterteilt aus denen ihr wählen könnt:

• Gleichung auflösen Aufgaben / Übungen
• Probe durchführen Aufgaben / Übungen
• Gleichungen mit Klammern Aufgaben / Übungen
• Bruchgleichungen Aufgaben / Übungen
• Ungleichungen Aufgaben / Übungen
• Lineare Gleichungen Aufgaben / Übungen
• Gleichungen erkennen Aufgaben / Übungen
• Ausklammern und Faktorisieren Aufgaben / Übungen

Video Äquivalenzumformung

Fragen mit Antworten Äquivalenzumformungen