Baumdiagramm und Pfadregeln

Was das Baumdiagramm ist und wie die Pfadregeln funktionieren, lernt ihr hier. Dies sehen wir uns an:

• Eine Erklärung, wofür man Baumdiagramme und Pfadregeln braucht.
• Beispiele der Wahrscheinlichkeitsrechnung zu beidem.
• Aufgaben / Übungen damit ihr dies selbst üben könnt.
• Ein Video zum Baumdiagramm
• Ein Frage- und Antwortbereich zu diesem Thema.

Tipp: Wenn ihr die nächsten Inhalte nicht versteht, dann fehlen vielleicht ein paar Vorkenntnisse. Ist dies der Fall könnt ihr gerne noch in die Inhalte Zufallsexperiment und mehrstufiges Zufallsexperiment reinsehen.

Erklärung Baumdiagramm und Pfadregeln

Die Wahrscheinlichkeitsrechnung ist ein Gebiet der Mathematik. In diesem befasst man sich zum Beispiel mit Zufallsexperimenten. Dabei handelt es sich um ein Experiment, welches mehrere Ergebnisse hat und beliebig oft wiederholt werden kann. Zwei Ergebnisse können dabei nicht gleichzeitig eintreten und vor der Durchführung kann das Ergebnis nicht vorausgesagt werden.

Typische Zufallsexperimente sind das Werfen einer Münze oder das Würfeln eines Würfels. Wobei Münze und Würfel besondere Zufallsexperimente, denn aller Ergebnisse sind gleichwahrscheinlich:

• Die Münze hat zwei mögliche Ergebnisse: Zahl und Wappen.
• Der 6-seitige Würfel hat sechs mögliche Ergebnisse: 1, 2, 3, 4, 5 und 6.

Sowohl bei der Münze als auch beim Würfel sind alle Ergebnisse gleichwahrscheinlich. Dies nennt man Laplace-Experiment bzw. Laplace-Versuch.

Beispiel für Münze:

Wozu braucht man jetzt ein Baumdiagramm und die Pfadregeln?

Ein Baumdiagramm mit zwei Stufen sieht zum Beispiel so aus:

Wie man sehen kann entstehen beim Baumdiagramm verschiedene Pfade. Dabei kann man die Wahrscheinlichkeiten für einzelne Pfade mit den Pfadregeln berechnen.

Anzeige:

Beispiele Baumdiagramm mit Pfadregeln

Sehen wie uns ein Beispiel an. Dieses bezeichnen wir als Baumdiagramm mit zurücklegen. Was das bedeutet, lernt ihr im Beispiel.

Beispiel 1: Baumdiagramm mit zurücklegen

Wir haben einen Kasten. In diesem Kasten sind 3 grüne und 2 blaue Kugeln. Ihr greift in den Kasten um eine Kugel zu ziehen. Ihr zieht dabei blind, also ohne in den Kasten reinzuziehen. Sobald die erste Kugel gezogen wurde, schreibt ihr die Farbe der Kugel auf und werft die Kugel in den Kasten zurück. Danach zieht ihr ein zweites Mal.

1a) Zeichne das Baumdiagramm für die erste Ziehung.

1b) Zeichne das Baumdiagramm für die zweite Ziehung.

1c) Wie groß ist die Wahrscheinlichkeit erst eine grüne und dann eine blaue Kugel zu ziehen?

1d) Wie groß ist die Wahrscheinlichkeit bei zwei Mal ziehen mindestens eine blaue Kugel zu ziehen?

Lösung:

1a) Wir haben 3 grüne Kugeln und 2 blaue Kugeln in der Kiste. Es sind damit insgesamt 5 Kugeln bei 2 verschiedenen Kugelfarben. Wir zeichnen das Baumdiagramm mit zwei Pfaden: Ein Pfad für die grünen Kugeln und ein Pfad für die blauen Kugeln. Die Wahrscheinlichkeit eine grüne Kugel zu ziehen ist dabei 3/5 und für eine blaue Kugel 2/5.

1b) Nach dem Ziehen legen wir die Kugel zurück in die Kiste und ziehen erneut. Daher ist dies auch ein "Baumdiagramm mit zurücklegen". Für das zweite Ziehen sind damit erneut 3 grüne und 2 blaue Kugeln drin. Dies zeichnen wir an das erste Ziehen dran.

1c) Wie groß ist die Wahrscheinlichkeit erst eine grüne und dann eine blaue Kugel zu ziehen? Dazu markieren wir uns den Pfad für genau dieses Ereignis. Zuerst der Weg zur grünen Kugel und danach zur blauen Kugel. Im nächsten Baumdiagramm ist dies rot markiert:

Berechnet werden soll die Wahrscheinlichkeit dafür, dass erst grün und dann blau gezogen wird. Dies schreibt man mit P(gb). Die Berechnung ist ganz einfach. Alle Wahrscheinlichkeiten entlang des Pfades werden miteinander multipliziert.

Die Wahrscheinlichkeit für erst eine grüne Kugel und danach eine blaue Kugel ist damit 6 : 25 = 0,24.

1d) Wie groß ist die Wahrscheinlichkeit bei zwei Mal ziehen mindestens eine blaue Kugel zu ziehen? Dazu markieren wir alle Pfade auf denen mindestens ein Mal eine blaue Kugel gezogen wird:

• Erst grün, dann blau: P(gb)
• Erst blau, dann grün: P(bg)
• Erst blau, danach nochmal blau: P(bb)

Wir müssen nun die Wahrscheinlichkeit für jeden der Pfade berechnen. Dazu nehmen wir die 1. Pfadregel und multiplizieren bei jedem Pfad erst einmal alle Wahrscheinlichkeiten miteinander:

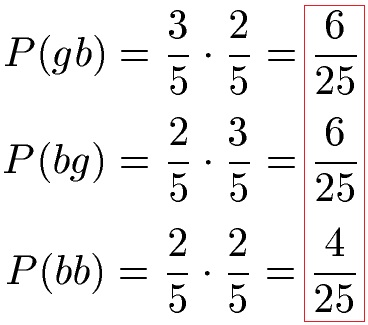
Wir kennen jetzt die Wahrscheinlichkeit für jeden einzelnen Pfad. Um die Gesamtwahrscheinlichkeit zu berechnen, müssen wir die einzelnen Wahrscheinlichkeiten addieren. Dies ist die 2. Pfadregel, auch Summenregel genannt.

Die Wahrscheinlichkeit bei zwei Mal ziehen mindestens ein Mal blau zu erwischen ist 16 : 25.

Aufgaben / Übungen Baumdiagramm

Aufgabe 1: Bevor wir rechnen kurz ein paar Fragen zum Baumdiagramm und den Pfadregeln. Mit der ersten Pfadregel berechnet man die Wahrscheinlichkeit für einen Pfad. Wie nennt man die Regel noch?

• Summenregel
• Quotientenregel
• Differenzregel
• Produktregel

Weiter zur Lösung » Aufgabe überspringen »

Du hast 0 von 4 Aufgaben erfolgreich gelöst.

Anzeigen:

Video Baumdiagramm

Fragen mit Antworten: Baumdiagramm und Pfadregel