Zinseszins berechnen: Formel, Beispiele und Erklärung

Was der Zinseszins ist und wie man damit rechnet, lernt ihr hier. Dies sehen wir uns an:

• Eine Erklärung, was Zinseszinsen sind und wie man diese mit Formeln berechnet.
• Beispiele zur Anwendung der Zinseszinsformeln (Anfangs- und Endkapital, Zinssatz und Anlagedauer).
• Aufgaben / Übungen um dieses Thema selbst zu üben.
• Ein Video zum Zinseszins.
• Ein Frage- und Antwortbereich zu diesem Gebiet.

Erklärung Zinseszins

Was versteht man unter dem Zinseszins? Starten wir mit einer kurzen Definition zu Zinseszinsen:

Wie kann man sich den Zinseszins nun vorstellen? Dazu nehmen wir einmal eine einfache Rechnung. Nehmen wir an, dass 2000 Euro für 3 Prozent Zinsen angelegt werden. Nehmen wir die Formel für die Berechnung der Jahreszinsen und setzen die Angaben ein, dann erhalten wir nach einem Jahr 60 Euro Zinsen. Auf die 2000 Euro kommen 60 Euro drauf. Nach einem Jahr haben wir damit 2060 Euro.

Wir legen die 2060 Euro für ein 2. Jahr an, erneut zu 3 Prozent. Dann erhalten wir 61,80 Euro an Zinsen. Dies liegt daran, dass die Zinsen vom 1. Jahr sich im 2. Jahr ebenfalls verzinst haben. Genau dies ist der Zinseszins: Die Zinsen pro Jahr steigen.

Die Rechnung von eben war nur für zwei Jahre. Die nächste Tabelle zeigt den Zinseszins, wenn man das Geld für viele weitere Jahre anlegt und jedes Jahr 3 Prozent Zinsen erhält. Wie man hier sehen kann, wächst das Kapital damit immer schneller. Jedes Jahr kommt eine größere Menge an Zinsen drauf.

Wie man aus der Tabelle vom Zinseszins sehen kann, wachsen Kapital und Zinsen immer schneller an. Dabei ist es sehr aufwändig das Kapital und die Zinsen für jedes Jahr einzeln zu berechnen. Schneller geht es mit entsprechenden Formeln.

Zinseszins Formel für Endkapital:

Dabei ist:

• "K_neu" ist das Kapital nach der Verzinsung (Endkapital)
• "K" ist das Kapital vor der Verzinsung (Anfangskapital)
• "p" ist die Zinszahl
• "n" ist die Anzahl der Jahre

Hinweis: Es gibt verschiedene Formeln zum Zinseszins und diese haben oftmals unterschiedliche Variablen (Buchstaben) im Einsatz. Bitte daher nicht wundern, wenn andere Quellen andere Formeln zeigen.

Stellen wir die Formeln für den Zinseszins noch um. Grund: Manchmal wird nicht nach dem Endkapital (Kapital nach Verzinsung) gefragt, sondern nach dem Anfangskapital (Kapital vor Verzinsung), nach den Höhe des Zinssatzes oder nach der Anzahl der Jahre.

Zinseszins-Formel umgestellt nach Anfangskapital:

Es folgt die Zinseszins-Formel umgestellt nach dem Anfangskapital K. Im Zähler steht das Endkapital (K_neu). Im Nenner wird (1 + p : 100) gerechnet hoch der Anzahl der Jahre n.

Zinseszins-Formel nach Zinszahl / Zinssatz umgestellt:

Als nächstes findet ihr die Formel für den Zinseszins, umgestellt nach der Zinszahl p. Dabei muss die n-te Wurzel gezogen werden aus dem Endkapital geteilt durch das Anfangskapital. Davon wird 1 abgezogen. Im Anschluss wird alles mit 100 multipliziert. Beispiel weiter unten.

Zusammenhang Zinssatz / Zinszahl:

Den Zinssatz könnt ihr berechnen, indem ihr die Zinszahl durch 100 dividiert.

Umstellen Zinseszins-Formel nach Anzahl der Jahre:

Als letzte Umstellung wird die Zinseszins-Formel nach der Anzahl der Jahre umgestellt. Im Zähler haben wir dabei den Logarithmus (lg) aus dem Endkapital durch das Anfangskapital. Im Nenner haben wir den den Logarithmus aus 1 + der Prozentzahl durch 100. Beispiel weiter unten.

Anzeige:

Beispiele Zinseszins

In diesem Abschnitt sehen wir uns typische Beispiele zum Zinseszins an.

Beispiel 1: Endkapital berechnen

Eine Summe von 3500 Euro wird zu einem Zinssatz von 4 Prozent für einen Zeitraum von 3 Jahren angelegt. Wie hoch ist das Endkapital?

Lösung:

Der Aufgabenstellung entnehmen wir das Anfangskapital K = 3500 Euro, die Zinszahl p = 4 und die Anzahl der Jahre n = 3. Dies setzen wir in die Gleichung ein und berechnen zunächst den Inhalt der Klammer. Diese wird mit der Potenz hoch 3 als nächstes ausgerechnet und als Letztes erfolgt die Multiplikation mit dem Startkapital. Nach der Verzinsung beträgt das Endkapital 3937,02 Euro.

Beispiel 2: Anfangskapital berechnen

Nach einer Anlagezeit von 7 Jahren schreibt die Bank einen Betrag von 14071 Euro gut. Dieses wurde zu 5 Prozent verzinst. Wie viel Geld wurde am Anfang angelegt?

Lösung:

Das Endkapital (nach der Verzinsung) sei K_neu = 14071 Euro. Die Anlagezeit ist n = 7 und es wurde zu 5 % angelegt, daher p = 5. Wir setzen dies in die Gleichung vom Zinseszins ein, welche nach dem Anfangskapital K umgestellt wurde. Dabei berechnen wir zunächst die Klammer im Nenner zu 1,05. Wir berechnen die Potenz 1,05⁷ und am Ende den Bruch. Das Anfangskapital / Startkapital lag damit bei 10.000 Euro.

Beispiel 3: Zinssatz / Zinszahl berechnen

Nach 5 Jahren wurden aus 2000 Euro Anlagesumme eine Endsumme von 2102,02 Euro. Wie hoch war der Zinssatz / die Zinszahl?

Lösung:

Die Anzahl der Jahre ist n = 5. Die Anfangssumme liegt bei K = 2000 Euro und die Endsumme K_end = 2102,02 Euro. Diese Angaben setzen wir in die Zinseszins-Formel ein, welche nach der Zinszahl p umgestellt wurde. Wir berechnen zunächst den Bruch unter der Wurzel zu 1,05101. Danach ziehen wir (mit dem Taschenrechner) die fünfte Wurzel aus 1,05101 und erhalten 1,01. Davon ziehen wir die 1 ab und erhalten 0,01 aus der Klammer. Wir multiplizieren mit 100 und erhalten die Zinszahl zu p = 1. Der Zinssatz ist damit p % = 1 %.

Beispiel 4 Zinseszins: Jahre berechnen

Eine Summe von 6800 Euro wurde mit 5 % Zinsen zu 8265,44 Euro. Wie viele Jahre hat das gedauert?

Lösung:

Das Anfangskapital sei K = 6800 Euro und die Zinszahl p = 5. Das Endkapital sei K_end = 8265,44 Euro. Wir setzen die Angaben in die Formel ein, welche nach n umgestellt wurde. Wir rechnen danach in Zähler und Nenner erst einmal die Klammern aus. Mit dem Taschenrechner berechnen wir danach den Logarithmus in Zähler und Nenner. Einmal den Logarithmus lg(1,2155) und den Logarithmus lg(1,05). Wir rechnen den Bruch aus und erhalten 4 Jahre Anlagedauer.

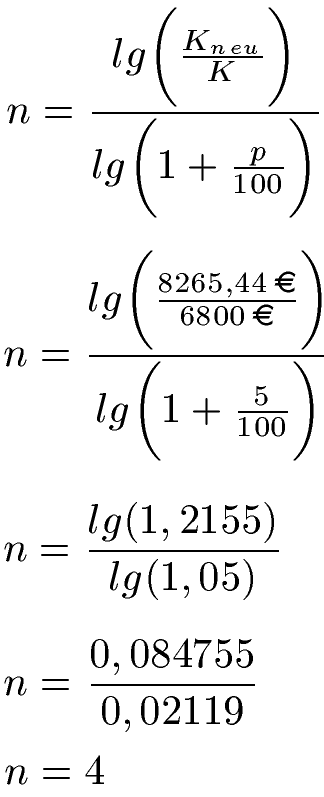
Aufgaben / Übungen Zinseszins

Aufgabe 1: Bevor wir rechnen kurz ein paar Fragen zur Formeln (Wer diese nicht will klickt auf überspringen). Zur ersten Frage: Wofür steht das K_neu in der nächsten Gleichung?

• Das Anfangskapital
• Das Endkapital
• Der Zinssatz
• Die Anzahl der Jahre

Weiter zur Lösung » Aufgabe überspringen »

Du hast 0 von 8 Aufgaben erfolgreich gelöst.

Anzeigen:

Video Zinseszins

Fragen mit Antworten Zinseszins