Prozentrechnung

Die Prozentrechnung wird hier behandelt. Dies sehen wir uns an:

• Eine Erklärung, was man mit der Prozentrechnung macht und was wichtig ist.
• Viele Beispiele zum Berechnen von Grundwert, Prozentwert und Prozentsatz.
• Aufgaben / Übungen um die Prozentrechnung selbst zu üben.
• Mehrere Videos zum Gebiet der Prozentrechnung.
• Ein Frage- und Antwortbereich zum Prozentrechnen.

Hinweis: Wir sehen uns hier das Thema Prozentrechnung relativ umfangreich an. Wer hingegen nur die Formeln sucht und wie man in diese etwas einsetzen kann, der findet dies auch verkürzt unter Prozentrechnung Formeln.

Prozentrechnung Erklärung

Was ist überhaupt die Prozentrechnung? Beginnen wir mit einer Definition:

Beispiel Prozent:

Angenommen wir haben 100 Äpfel. Dann sind 1 % von diesen Äpfeln nur 1 Apfel, also 1 von 100. Möchten wir hingegen 12 % haben, dann sind dies 12 von 100 Äpfel. Mathematisch schreibt man dies so:

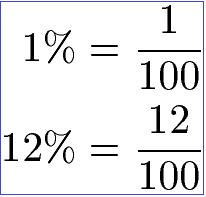
Wichtige Begriffe der Prozentrechnung:

Um mit Prozenten rechnen zu können, sollte man zunächst die wichtigsten Begriffe der Prozentrechnung kennen und verstehen. Diese sind:

• Grundwert: Unter dem Grundwert versteht man "das Ganze" auf das sich die Prozentangaben beziehen, zum Beispiel alle Personen, das Ganze Geld oder der komplette Inhalt einer Flasche. In den meisten Fällen entspricht alles 100 Prozent. In Formeln wird der Grundwert mit einem G oder GW abgekürzt.
• Prozentwert: Unter dem Prozentwert versteht man einen Anteil an etwas Ganzem. Man spricht dabei auch von der Anzahl oder der absoluten Häufigkeit. Befinden sich 100 Personen in einem Raum von denen 60 männlich sind, dann ist 100 Personen der Grundwert und 60 der Prozentwert. In Formeln wird der Prozentwert für W oder PW eingesetzt.
• Prozentsatz: Der Prozentsatz p% gibt einen Anteil an einem Grundwert an. Ein Preisnachlass von 40 % auf ein Produkt für 100 Euro bedeutet, dass dieses Produkt 40 Euro billiger wird. In diesem Fall wäre der Grundwert G = 100 Euro und der Prozentsatz p % = 40 %. In Formeln ist der Prozentsatz p %.
• Prozentzahl: In manchen Formeln wird nicht der Prozentsatz p % verwendet, sondern nur die Prozentzahl p, also ohne Prozentzeichen.

Die nächste Gleichung zeigt den Zusammenhang zwischen Prozentzahl p und Prozentsatz p %. Wie man damit umgeht, behandeln wir weiter unten bei den Formeln.

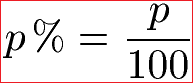
Anzeige:

Beispiele Prozentrechnung: Grundwert, Prozentwert und Prozentsatz

Wir hatten eben die wichtigsten Begriffe der Prozentrechnung. Nun wird es wichtig, diese auch in der Praxis einsetzen zu können. Dazu sehen wir uns die Formel bzw. Formeln der Prozentrechnung an sowie diese umgestellt nach den jeweiligen Variablen (Buchstaben).

Grundwert der Prozentrechnung:

Starten wir mit dem Grundwert der Prozentrechnung. Darunter versteht man das Ganze, auf welche sich der Anteil und der Prozentsatz beziehen. Die Formel um den Grundwert zu berechnen lautet:

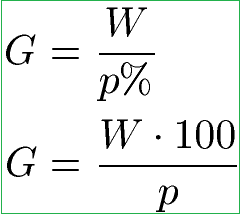
Wir erhalten den Grundwert G, indem wir den Prozentwert W durch den Prozentsatz p % teilen. Alternativ können wir auch den Prozentwert W mit 100 multiplizierten und durch die Prozentzahl p teilen.

Beispiel 1 zum Grundwert:

Anna hat in diesem Monat 12 Euro ihres Taschengeldes ausgegeben. Dies sind 30 Prozent ihres Taschengeldes. Wie viel Geld bekommt sie jeden Monat?

Lösung:

Gesucht ist "das Ganze", also der Grundwert G. Wir wissen, dass ein Anteil von W = 12 Euro gegeben ist. Dies sind 30 Prozent, daher ist p = 30. Wir setzen dies in die Gleichung von oben ein und rechnen die Zahlen aus. Die Währung (Euro) darf nicht vergessen werden.

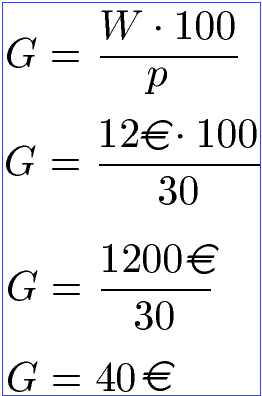
Anna bekommt 40 Euro Taschengeld im Monat.

Weitere Beispiele zur Berechnung vom Prozentwert findet ihr unter Prozentwert berechnen.

Prozentwert der Prozentrechnung:

Der Prozentwert W gibt den Anteil an etwas Ganzem an. Die Formel bzw. Formeln um den Prozentwert zu berechnen lauten:

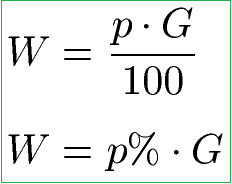
Wir erhalten den Prozentwert W, indem wir die Prozentzahl mit dem Grundwert multiplizieren und durch 100 teilen. Alternativ können wir den Prozentwert W berechnen, in dem wir den Prozentsatz mit dem Grundwert multiplizieren.

Beispiel 2 zum Prozentwert:

Ein Fahrrad kostet im Normalfall 500 Euro. Der Händler bietet es aktuell jedoch mit einem Rabatt von 15 Prozent an. Wie viel Euro beträgt der Rabatt?

Lösung:

Das Rad kostet normalerweise 500 Euro, was dem Gesamtpreis entspricht. Dies ist der Grundwert, daher ist G = 500 Euro. Der Preisnachlass beträgt 15 Prozent, daher p% = 15% bzw. p = 15. Diese Angaben setzen wir in eine der beiden Gleichungen ein.

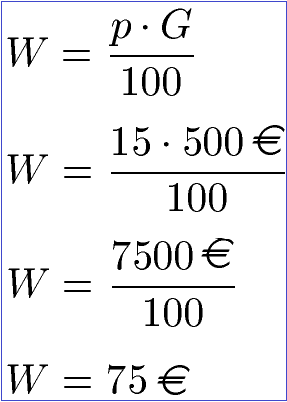
Das Fahrrad gibt es mit 75 Euro Rabatt.

Hinweis zur Aufgabe: Bei dieser Aufgabe haben wir die Formel mit p und nicht mit p% genommen. Der Hintergrund ist ganz einfach. Würden wir die Formel mit p % verwenden müssten wir 15 % einsetzen und 15 % ist nicht anderes als 15 : 100. Wir würden damit exakt die gleichen Rechenschritte durchführen. Warum also nicht gleich die direkte Formel nehmen?

Weitere Beispiel zur Berechnung vom Prozentwert findet ihr unter Prozentwert berechnen.

Formeln zum Prozentsatz / zur Prozentzahl:

Fehlen uns noch Prozentsatz und Prozentzahl. Der Prozentsatz p% gibt einen Anteil an einem Grundwert an. Die Prozentzahl p wird ohne Prozentzeichen angegeben. Die Formeln sehen wie folgt aus:

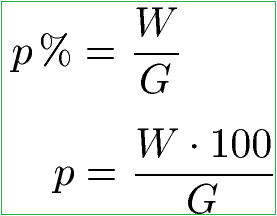
Den Prozentsatz kann man berechnen, indem man den Prozentwert durch den Grundwert dividiert. Alternativ kann man die Prozentzahl berechnen, indem man den Prozentwert mit 100 multipliziert und durch den Grundwert teilt.

Beispiel 3 zum Prozentsatz / Prozentzahl:

Clara wiegt derzeit 88 Kilo. Ihr Arzt empfehlt ihr, dass sie mindestens 7 Kilo abnehmen soll. Wie viel Prozent sind dies?

Lösung:

Clara muss knapp 8 Prozent abnehmen.

Weitere Beispiele und Aufgaben zum Prozentsatz bzw. der Prozentzahl findet ihr unter Prozentsatz / Prozentzahl berechnen.

Aufgaben / Übungen Prozentrechnung

Aufgabe 1: Bevor rechnen kurz ein paar Fragen zu den Formeln. Wer diese nicht mag, kann auch auf überspringen klicken um zu den Rechenaufgaben zu kommen. Zur nächsten Formel: Wofür steht das "G" in den Formeln der Prozentrechnung?

• Prozentwert
• Prozentzahl
• Grundwert
• Prozentsatz

Weiter zur Lösung » Aufgabe überspringen »

Du hast 0 von 11 Aufgaben erfolgreich gelöst.

Anzeigen:

Video Prozentrechnung