Brüche subtrahieren

Wie man Brüche subtrahiert, lernt ihr hier. Dies sehen wir uns an:

• Eine Erklärung, wie man gleichnamige, ungleichnamige und gemischte Brüche subtrahiert.
• Viele Beispiele zum Subtrahieren von Brüchen.
• Aufgaben / Übungen zur Subtraktion beim Bruchrechnen.
• Ein Video zu diesem Thema.
• Ein Frage- und Antwortbereich zum Brüche subtrahieren.

Ein kleiner Tipp zum Start: Wenn ihr nicht wisst, was ein Bruch ist, werft bitte erst einmal einen Blick in den Hauptartikel Bruchrechnen. Ansonsten ran an das Thema.

Erklärung Brüche subtrahieren

Wie funktioniert dies mit dem Subtrahieren von Brüchen? Starten wir mit einem Beispiel.

Beispiel 1: Nehmen wir dazu eine Pizza und schneiden wir diese in 8 Stücke. Die Stücke sind alle gleich groß. Die nächste Grafik zeigt dies:

Die Pizza besteht aus 8 Stücken. Von diesen 8 Stücken essen wir nun 5 Stücke auf (rot markiert). Daher bleiben 3 Stücke übrig (grün markiert). Die nächste Grafik zeigt euch dies:

Wie kann man dies mit Brüchen ausdrücken? Eigentlich ganz einfach: Wir haben am Anfang 8 von 8 Stücke und essen 5 von 8 Stücke. Daher bleiben 3 von 8 Stücke übrig. Dies schreibt man so auf:

Wie man sehen kann: Hier wird bei den Zählern einfach eine Subtraktion durchgeführt. Der Nenner bleibt.

Anzeige:

Gleichnamige Brüche subtrahieren

In diesem Abschnitt sehen wir uns die Subtraktion von Brüchen für gleichnamige, ungleichnamige und gemischte Brüche an. Starten wir mit gleichnamigen Brüchen, also Aufgaben zur Subtraktion mit gleichem Nenner.

Beispiel 2:

Wie lautet die Lösung der nächsten Aufgabe?

Lösung:

Wir haben hier zwei gleichnamige Brüche, denn der Nenner ist bei beiden 5. Daher können wir einfach im Zähler subtrahieren. Der Nenner bleibt gleich.

Beispiel 3:

Wie lautet die Lösung der nächsten Aufgabe?

Lösung:

Auch hier haben wir gleichnamige Brüche. Daher können wir die Nenner einfach stehen lassen und im Zähler die Subtraktionen durchführen. 10 - 3 - 1 = 6. Wir erhalten damit 6/9 als Ergebnis. Dieses könnte man noch kürzen, dazu mehr weiter unten.

Die ersten drei Beispiele waren für gleichnamige Brüche. Die nächsten Beispiele beziehen sich auf ungleichnamige Brüche.

Ungleichnamige Brüche subtrahieren

Gleichnamige Brüche sind Brüche mit gleichen Nennern. Bei ungleichnamigen Brüchen sind die Nenner hingegen verschieden. Sehen wir uns Aufgaben bzw. Beispiele zu ungleichnamigen Brüchen an.

Beispiel 4:

Wie lautet die Lösung der nächsten Aufgabe?

Lösung:

Die Nenner sind verschieden. Wir dürfen hier daher nicht einfach Subtrahieren, sondern müssen erst einmal einen gemeinsamen Nenner finden. Die am einfachsten zu verstehende Methode soll dazu gezeigt werden. Der erste Schritt ist einen gemeinsamen Nenner zu finden. Dazu multiplizieren wir die beiden Nenner miteinander: 5 · 4 = 20. Der gemeinsame Nenner ist damit 20. Zum besseren Verständnis schreiben wir dies kurz hin:

Fehlen uns noch die Zähler. Der erste Bruch hatte eine 5 im Nenner. Wir müssen diese 5 mit 4 multiplizieren, um auf die 20 zu kommen. Daher multiplizieren wir den Zähler auch mit 4. Wir erhalten damit 3 · 4 = 12. Der zweite Bruch hatte eine 4 im Nenner. Um hier auf 20 zu kommen, musste mit 5 multipliziert werden. Dies machen wir auch im Zähler: 2 · 5 = 10.

Jetzt können wir einfach die Zähler subtrahieren. Der Nenner bleibt erhalten.

Hinweis: Diesen Bruch kann man noch kürzen. Wie dies funktioniert sehen wir uns weiter unten an.

Beispiel 5:

Die nächste Subtraktionsaufgabe umfasst drei Brüche. Wie rechnet man dies?

Lösung:

Wir haben hier drei verschiedene Nenner. Wir suchen daher einen gemeinsamen Nenner. Wir verwenden dazu das kleinste gemeinsame Vielfache. Dazu nehmen wir die drei Nenner und multiplizieren diese mit 1, 2, 3 und so weiter. Danach suchen wir die kleinste Zahl, die bei allen vorkommt. Dies ist die 18.

Um auf die 18 im Nenner zu kommen, müssen wir beim ersten Bruch mit 6 multiplizieren. Beim zweiten Bruch müssen wir mit 2 multiplizieren und beim dritten Bruch müssen wir nichts machen (Multiplikation mit 1). Genau dies machen wir exakt so auch im Zähler.

Jetzt können wir einfach im Zähler subtrahieren. Der Nenner bleibt wie immer.

Diesen Bruch kann man noch kürzen. Wie dies funktioniert sehen wir weiter unten.

Anzeigen:

Gemischte Brüche subtrahieren

Kümmern wir uns noch um die Subtraktion von gemischten Zahlen / gemischten Brüchen. Um diese Subtrahieren zu können, wandeln wir diese zunächst in ganz normale Brüche um und Subtrahieren diese im Anschluss.

Beispiel 6:

Wie lautet die Lösung der nächsten Aufgabe?

Lösung:

Das Umwandeln ist ganz einfach. Wir multiplizieren im Zähler die Zahl vor dem Bruch mit dem Nenner und behandeln den Nenner bei. Darauf addieren wir noch den Bruch.

Die Aufgabe sieht dann wie folgt aus:

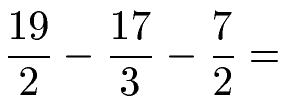
Wir haben jetzt leider noch verschiedene Nenner. Daher brauchen wir einen gemeinsamen Nenner. Mit 2 · 3 = 6 erhalten wir diesen. Daher multiplizieren wir den ersten Bruch und den dritten Bruch mit 3 und den mittleren Bruch mit 2.

Auch diesen Bruch könnte man noch kürzen. Wie man kürzt sehen wir uns im nächsten Abschnitt noch an.

Brüche kürzen

Man kann Brüche in manchen Fällen kürzen. Kürzen bedeutet den Zähler und den Nenner durch die gleiche Zahl zu teilen. In der Regel macht man dies nur für natürliche Zahlen. Ob die Zahl im Zähler und im Nenner durch eine andere (natürliche) Zahl ohne Rest teilbar ist, kann man mit den Teilbarkeitsregeln raus finden. Wobei man bei kleineren Zahlen dies oft auf den ersten Blick sieht. Dazu ein Beispiel.

Beispiel 7:

Hier seht ihr ein paar Beispiele für das Kürzen von Brüchen. Der erste Bruch wurde mit 2 gekürzt (Zähler und Nenner durch 2 ohne Rest teilbar). Der zweite Bruch wurde mit 3 gekürzt (Zähler und Nenner ohne Rest durch 3 teilbar).

Übungsaufgaben Brüche subtrahieren

Aufgabe 1: Wie lautet das Ergebnis?

• 3 / 8
• 1 / 5
• 3 / 5
• 4 / 5

Weiter zur Lösung » Aufgabe überspringen »

Du hast 0 von 6 Aufgaben erfolgreich gelöst.

Video Subtraktion Brüche

Fragen mit Antworten Brüche subtrahieren