Bruchrechnen

Das Bruchrechnen - also das Rechnen mit Brüchen - zeigen wir euch hier. Dies sehen wir uns an:

• Eine Erklärung, was ein Bruch ist und wie man mit diesem rechnet.
• Viele Beispiele zur Addition, Subtraktion, Multiplikation und Division von Brüchen sowie Kürzen und Erweitern.
• Aufgaben / Übungen zum Bruchrechnen
• Ein Video zum Thema.
• Ein Frage- und Antwortbereich zur Bruchrechnung.

Ein kleiner Tipp zum Start: Wir werden gleich sehen, dass ein Bruch nichts anderes als eine Division ist. Wer also das Teilen - wie zum Beispiel 3 : 4 - nicht kennt, der kann sich dies kurz noch unter Dividieren / Teilen ansehen.

Bruchrechnen: Was ist ein Bruch?

Zunächst sollten wir erst einmal die Grundlagen zur Bruchrechnung behandeln: Was ist ein Bruch? Nehmen wir an ihr esst Brötchen. Dann könnt ihr 1 Brötchen essen oder 2 Brötchen oder auch 3. Aber manchmal isst man kein ganzes Brötchen, sondern nur einen Teil von einem Brötchen. Oder man schafft es nur einen Teil einer Pizza zu essen. So etwas muss man natürlich auch in der Mathematik irgendwie aufschreiben können. Genau dies macht man mit einem Bruch.

Wie kann man die Bruchrechnung für Kinder oder Anfänger in diesem Thema einfach darstellen? Nehmen wir eine Pizza. Diese Pizza schneiden wir in 8 gleich große Stücke:

Angenommen wir essen nun 5 von 8 Stücken. Dann drückt man dies in der Mathematik mit einem Bruch aus. In diesem Fall schreibt man dies mit

Markieren wir die 5 Stücke einmal in rot (und den Rest in grün) :

Essen wir die 5 Stücke (rot markiert) bleiben noch 3 Stücke übrig. Diese 3 von 8 Stücke kann man natürlich ebenfalls als Bruch schreiben.

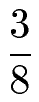
Kommen wir noch zu den Begriffen beim Bruchrechnen: Wir haben eine Zahl, die oben steht. Dann einen Strich und darunter noch eine Zahl. Man bezeichnet die Zahl oben als Zähler, die Zahl unten als Nenner und dazwischen gibt es einen Bruchstrich.

Die Definition zur Bruchrechnung:

Anzeige:

Rechnen mit Brüchen, kürzen und erweitern

In den Grundlagen weiter oben wurde bereits erwähnt, dass man mit Brüchen auch Rechnen kann. Genau dies soll hier einmal passieren. Dabei sehen wir uns alle Grundrechenarten an. Dies sind jeweils Beispiele mit Rechenwegen und Lösungen.

Beispiel 1: Brüche Addieren

Wir schneiden eine Torte in 9 gleich große Stücke. Anna isst 3 Stücke und Marc isst 4 Stücke. Wie schreibt man dies als Bruch? Wie viele Stücke wurden am Ende gegessen?

Lösung:

Wir schreiben zunächst beide Angaben als Bruch. Dies sind 3 von 9 Stücke und 4 von 9 Stücke. Diese addieren wir, sprich zwischen die beiden Brüche kommt ein Pluszeichen. Da die Nenner - also die Zahlen unten - gleich sind, können wir einfach die Zähler addieren.

Am Ende wurden damit 7 von 9 Stücken gegessen.

Hinweis: Den Umgang mit unterschiedlichen Nennern lernen wir weiter unten.

Beispiel 2: Brüche subtrahieren

Die Umkehrung der Addition ist die Subtraktion. Wir sehen uns nun das "Minusrechnen" bei Brüchen an. Dazu nehmen wir an, dass eine Torte in 12 Stücke zerschnitten wurde. Alle Teile sind gleich groß und wurden den Gästen angeboten. Die Gäste essen 7 Stücke auf. Wie viele Stücke Torte bleiben übrig?

Lösung des Beispiels:

Wir haben am Anfang eine ganze Torte mit 12 Stücken, die den Gästen gegeben wurde. 12 von 12 Stücke bekamen diese vorgesetzt. 7 von 12 Stücke wurden gegessen. Wir müssen daher von den 12 Stücken 7 Stücke abziehen.

Es bleiben 5 von 12 Stücken übrig.

Auch hier der Hinweis: Den Umgang mit verschiedenen Nennern sehen wir uns weiter unten an.

Beispiel 3: Brüche multiplizieren

Die nächste Grundrechenart ist die Multiplikation, also das Malnehmen von zwei (oder mehr) Brüchen. Manche Personen bezeichnen dies auch als "Bruchrechnen mal". Die Berechnung dabei ist eigentlich ganz einfach. Zähler wird mit Zähler multipliziert und Nenner wird mit Nenner multipliziert.

Beim Multiplizieren von Brüchen kommt es oft vor, dass Brüche gekürzt werden können. Was das ist und wie es funktioniert behandeln wir weiter unten.

Beispiel 4: Brüche dividieren

Die letzte Grundrechenart ist die Division. Es geht darum Brüche zu dividieren. Dabei haben wir zwei Brüche zwischen denen ein Geteiltzeichen stehen. Die Berechnung sieht so aus, dass man den zweiten Bruch umdreht (Zähler und Nenner vertauscht, in rot markiert). Man nennt dies den Kehrwert bilden. Nach Bildung des Kehrwerts werden die beiden Brüche miteinander multipliziert (Zähler mal Zähler und Nenner mal Nenner).

Im nächsten Abschnitt lernt ihr, wie man so ein Ergebnis noch kürzen kann.

Beispiel 5: Brüche kürzen

In diesem Abschnitt geht es um das Kürzen von Brüchen. Darunter versteht man ganz einfach den Zähler und den Nenner durch die gleiche Zahl zu dividieren. Dies macht man im Normalfall dann, wenn man im Zähler und Nenner jeweils natürliche Zahlen hat und beide durch eine andere natürliche Zahl ohne Rest teilbar sind. Damit vereinfacht man den Bruch.

Ob dies der Fall ist, kann man entweder einfach ausprobieren, indem man durch 2, 3, 4 etc. im Kopf teilt oder auch die Teilbarkeitsregeln anwendet. Ein Beispiel soll dies verdeutlichen. So wurde der nächste Bruch mit 3 gekürzt, denn Zähler und Nenner wurden jeweils durch 3 geteilt.

Beim nächsten Bruch wurde zunächst mit 2 gekürzt und im Anschluss wird erneut gekürzt (mit 3). Dies bedeutet, dass zunächst Zähler und Nenner jeweils durch 2 geteilt wurden und im Anschluss noch einmal durch 3 geteilt wurde.

Beispiel 6: Brüche erweitern

Beim Brüche kürzen wurden Zähler und Nenner jeweils durch eine Zahl geteilt. Beim Brüche erweitern passiert das Umgekehrte: Brüche werden erweitert, indem Zähler und Nenner jeweils mit einer Zahl (oder Variablen) multipliziert werden. Als Beispiel soll einmal ein Bruch mit 5 erweitert werden. Daher multiplizieren wir Zähler und Nenner jeweils mit 5.

Beispiel 7: Hauptnenner finden

Man unterscheidet in der Bruchrechnung gleichnamige und ungleichnamige Brüche. Gleichnamige Brüche haben alle den gleichen Nenner (zum Beispiel alle den Nenner 3). Ungleichnamige Brüche haben verschiedene Nenner. Bei den Additionen und Subtraktionen von Brüchen weiter oben hatten wir gleichnamige Nenner. Daher durften wir hier ganz einfache die Zähler addieren oder subtrahieren.

Hat man jedoch verschiedene Nenner, dann muss man zunächst einen gemeinsamen Nenner suchen, man nennt diesen Hauptnenner. Wir müssen also dafür sorgen, dass alle Brüche den gleichen Nenner haben. Es gibt verschiedene Möglichkeiten, dies zu tun. Der am einfachsten Verständliche Weg soll hier einmal gezeigt werden. Berechnet werden soll:

Wir haben hier 3 und 4 als Nenner. Ein einfacher Weg einen gemeinsamer Nenner zu finden ist diese beiden Zahlen einfach zu multiplizieren. 3 · 4 = 12.

Was machen wir jetzt mit den Zählern? Nun, beim ersten Bruch mussten wir den Nenner mit 4 multiplizieren, um auf die 12 zu kommen. Dies machen wir auch mit dem Zähler: 2 · 4 = 8. Beim zweiten Nenner mussten wir die 4 mit 3 multiplizieren, um auf die 12 zu kommen. Dies machen wir nun auch mit dem Zähler: 3 · 3 = 9.

Jetzt können wir einfach die Zähler addieren (und den Nenner übernehmen).

Aufgaben / Übungen Bruchrechnen

Aufgabe 1: Bevor wir Rechnen ganz kurz ein paar einfache Fragen. Wer diese nicht mag, kann aber gerne auf "überspringen" klicken. Zur ersten Frage: Wie nennt man die Zahl oberhalb vom Bruchstrich?

• Quadratzahl
• Zähler
• Nenner
• Wurzelzahl

Weiter zur Lösung » Aufgabe überspringen »

Du hast 0 von 8 Aufgaben erfolgreich gelöst.

Anzeigen:

Videos Bruchrechnung

Fragen mit Antworten Bruchrechnung