Eulersche Zahl

Die eulersche Zahl behandeln wir hier. Dies sehen wir uns an:

• Eine Erklärung, was die Eulersche Zahl ist.
• Beispiele zu dieser speziellen Zahl.
• Aufgaben / Übungen zu diesem Thema.
• Ein Video bei dem die Eulersche Zahl vorkommt.
• Ein Frage- und Antwortbereich zu diesem Thema.

Tipp: In der Mathematik gibt es verschiedene Konstanten. Die Eulersche Zahl ist eine davon. Deutlich bekannter sollte jedoch die Kreiszahl Pi sein.

Eulersche Zahl Erklärung

In der Mathematik gibt es so genannte Konstanten, welche in Gleichungen verwendet werden können. Am Bekanntesten dürfte die Kreiszahl Pi sein. Pi wird benötigt um zum Beispiel die Fläche von einem Kreis zu berechnen. Diese Kreiszahl ist etwas größer als 3:

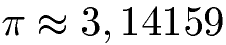
Neben der Kreiszahl Pi gibt es noch eine weitere Konstante, welche sehr oft in der Mathematik verwendet wird. Diese wird als Eulersche Zahl bezeichnet. In Formeln / Gleichungen wird diese mit einem "e" abgekürzt. Diese Zahl ist etwas größer als 2,71.

Beispiel:

Wie groß ist x in der nächsten Gleichung?

Lösung:

Wir setzen für e = 2,718282 ein und lösen im Anschluss die Gleichung nach x auf.

Anzeige:

Eulersche Zahl Anwendung

Wofür braucht man die Eulersche Zahl eigentlich?

E-Funktion:

• Funktionen können die Eulersche Zahl beinhalten.
• Beispiel f(x) = e^x.

Ableiten und Integrieren:

• In der 10. Klasse und in der Oberstufe wird die sogenannte Integral- und Differentialrechnung behandelt.
• Dabei befasst man sich mit der Steigung einer Funktion oder der Fläche unter einer Funktion.
• Dabei kann in manchen Fällen auch die E-Funktion mit der Eulerschen Zahl vorkommen.
• Das besondere daran ist, dass "e" abgeleitet oder integriert "e" bleibt.

Wachstum:

• Eine Reihe von Wachstumsvorgängen (und auch Abklingvorgängen) in der Natur können mit Gleichungen beschrieben werden, welche die Zahl "e" beinhaltet.

Physik:

• Einige Vorgänge in der Physik / Technik beinhalten Funktionen, die auf "e" basieren.
• Zum Beispiel in der Strömungslehre.

Logarithmus:

• Der natürliche Logarithmus ist die Umkehrung der E-Funktion.
• Ein Beispiel dazu findet ihr in den Logarithmengleichungen.

Aufgaben / Übungen Eulersche Zahl

Aufgabe 1:

Starten wir zunächst mit ein paar einfachen Fragen. Danach wird auch ein bisschen gerechnet. Wer die Fragen nicht mag kann auch direkt auf "überspringen" klicken.

• Wie wird die Eulersche Zahl in Formeln abgekürzt?

• y
• x
• a
• e

Weiter zur Lösung » Aufgabe überspringen »

Du hast 0 von 3 Aufgaben erfolgreich gelöst.

Anzeigen:

Video E-Funktion

Fragen mit Antworten Eulersche Zahl