Bruchrechnung Textaufgaben / Sachaufgaben

Zur Bruchrechnung bekommt ihr hier Textaufgaben bzw. Sachaufgaben. Im Artikel werden diese vorgerechnet, zusätzlich bekommt ihr Aufgaben zum Selbst üben. Dies sehen wir uns an:

• Eine Erklärung, wie man mit Textaufgaben bei der Bruchrechnung umgeht.
• Viele Beispiele zum Lösen von Textaufgaben.
• Aufgaben / Übungen damit ihr das Thema selbst üben könnt.
• Videos zur Bruchrechnung.
• Ein Frage- und Antwortbereich zu diesem Gebiet.

Hinweis: Wenn ihr nicht wisst, was ein Bruch mit Zähler und Nenner ist, werft bitte erst einmal einen Blick in den Hauptartikel Bruchrechnen. Ansonsten ran an die Textaufgaben.

Erklärung Textaufgaben Bruchrechnung

Starten wir mit relativ einfachen Aufgaben zur Bruchrechnung, um einen Einstieg zu bekommen.

Beispiel 1: Einfache Textaufgabe
Kevin hat 50 Euro gespart. Er gibt 2/5 für Süßigkeiten aus. Wie viel Geld hat er ausgegeben?

Lösung:
Wir nehmen die 50 Euro und davon 2 von 5 Teile. Dies bedeutet, dass wir den Geldbetrag mit 2/5 multiplizieren müssen.

Antwort: Kevin hat 20 Euro von 50 Euro ausgegeben.

Beispiel 2: Mittelschwere Aufgabe
Jacob bemalt Tische. Er hat von einem Farbtopf derzeit 7 : 8 übrig. Für jeden Tisch benötigt er 1 : 16 des Topfes. Wie viele Tische kann er bemalen?

Lösung:
Wir schreiben zunächst die Teilungsaufgabe auf. Danach multiplizieren wir mit dem Kehrwert. Das Ergebnis können wir berechnen. Wir erhalten damit 14 als Lösung.

Antwort: Der Topf langt damit für 14 Tische.

Beispiel 3: Schwierige Aufgabe Bruchrechnung
Anna möchte sich ein neues Fahrrad kaufen. Sie hat 240 Euro gespart. Dies sind 3/5 des Preises, den das Fahrrad gerade kostet. Erst drei Tage später kommt sie ins Fahrradgeschäft. Das Rad ist in dieser Zeit um 20 Euro teurer geworden. Was kostet das Fahrrad jetzt?

Lösung:
Wir beginnen mit diesem Satz: "Sie hat 240 Euro gespart. Dies sind 3/5 des Preises, den das Fahrrad gerade kostet." Wir wissen nicht, was das Fahrrad kostet. Dies bezeichnen wir als "x" in der Gleichung. Wir setzen den Text direkt in eine Gleichung um.

Das x ist nun der gesuchte Preis. Diesen müssen wir berechnen. Wir müssen daher die Gleichung so verändern, dass wir "x = ..." erhalten. Auf der rechten Seite der Gleichung teilen wir durch 5. Die Umkehrung der Division ist die Multiplikation. Daher müssen wir mit 5 multiplizieren.

Auf der rechten Seite steht noch 3 · x. Die Umkehrung einer Multiplikation ist die Division. Daher müssen wir durch 3 teilen.

Dies rechnen wir nun aus:

Dies war der ursprüngliche Preis. Das Rad wurde 20 Euro teurer. Diese 20 Euro müssen wir auf die 400 Euro noch drauf addieren.

Lösung: Das Fahrrad kostet beim Kauf 420 Euro.

Beispiel 4: Schwierige Aufgabe Bruchrechnung
Frau Liebig verdient im Monat netto 1614 Euro. Sie braucht ein Drittel dieses Geldes für die monatliche Miete. Die Miete ist in den letzten 6 Jahren um 1/5 gestiegen. Was bezahlt Frau Liebig aktuell an Miete? Was bezahlte sie vor 6 Jahren?

Lösung:
Die Frau gibt 1/3 des Geldes für die Miete aus. Daher nehmen wir die 1614 Euro und multiplizieren dies mit 1/3.

Antwort Teil 1: Frau Liebig bezahlt aktuell 538 Euro an monatlicher Miete.

Der zweite Teil der Frage war, wie hoch die Miete vor 6 Jahren war. Wenn wir das Rechnen sollte jedem zuerst klar sein, dass die Miete damals niedriger war. Die Miete ist gestiegen. Bekommen wir beim Ergebnis mehr als 538 Euro heraus, ist etwas schief gelaufen.

Wie rechnet man dies nun? Die Miete vor 6 Jahren kennen wir nicht, daher schreiben wir einfach einmal x bei der Berechnung für diesen Betrag. Was wir aber wissen ist, dass die Miete um 1/5 höher ist als damals. Wir hatten daher damals eine Miete von x und diese ist um 1/5 nach oben gegangen. Die Miete damals war damit 1 (man könnte auch sagen 100 Prozent oder also Bruch geschrieben 5/5). Darauf müssen wir 1/5 drauf addieren. Wir haben damit 6/5 inzwischen. Diese 6/5 ist das, was sie heute bezahlen muss. Die Rechnung sieht damit so aus:

Das x müssen wir jetzt ausrechnen. Dazu müssen wir die Gleichung so verändern, dass das x alleine auf einer Seite der Gleichung steht. Wir brauchen "x = ..." als Antwort. Wir teilen auf der linken Seite der Gleichung durch 5. Die Umkehrung vom Teilen ist die Multiplikation, wir multiplizieren daher mit 5.

Auf der linken Seite multiplizieren wir das x mit der 6. Die Umkehrung der Multiplikation ist die Division. Wir teilen daher beide Seiten der Gleichung durch 6.

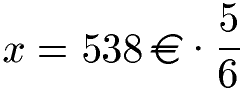
Wir rechnen die rechte Seite der Gleichung aus:

Antwort Teil 2: Frau Liebig bezahlte vor 6 Jahren noch 448,33 Euro für die Miete.

Anzeige:

Aufgaben / Übungen Textaufgaben

Aufgabe 1: Kevin hat 50 Euro gespart. Er gibt 2/5 für Süßigkeiten aus. Wie viel Geld hat er ausgegeben?

• 50 Euro
• 40 Euro
• 20 Euro
• 60 Euro

Weiter zur Lösung » Aufgabe überspringen »

Du hast 0 von 4 Aufgaben erfolgreich gelöst.

Video Bruchrechnung bei Textaufgaben

Anzeigen:

Fragen mit Antworten Sachaufgaben Bruchrechnung