Terme umformen / umstellen

Wie kann man Terme umformen (Weiterführendes Thema: Gleichungen lösen)? Dies sehen wir uns an:

• Eine Erklärung, wie die Termumformung funktioniert.
• Viele Beispiele zur Umformung von Termen.
• Aufgaben / Übungen damit ihr dies selbst üben könnt.
• Videos zum Umgang mit Termen.
• Ein Frage- und Antwortbereich zu diesem Thema.

Wir sehen uns gleich an, wie man mit Termen umgeht. Es hilft, wenn ihr bereits die Grundrechenarten kennt, also Addition, Subtraktion, Multiplikation und Division. Ihr solltet auch wissen, was eine Variable ist. Ihr wisst dies bereits? Dann ran an das Arbeiten mit Termen. Ansonsten bitte erst diese beiden Artikel kurz nachlesen.

Terme kann man auch miteinander vergleichen bzw. nach einer Variablen wie zum Beispiel x auflösen. Wen dies interessiert sieht noch in den Artikel Gleichungen lösen.

Erklärung Terme umformen

Wie funktioniert das Umformen und Zusammenfassen von Termen? Fangen wir dazu mit einer einfachen Regel an: Kommen bei Termen die gleichen Variablen vor, dann darf man diese zusammenfassen.

Dies funktioniert auch wenn zwei Variablen pro Term vorkommen:

Das dies mit der Zusammenfassung funktioniert sehen wir uns gleich einmal mit ein paar Zahlen an. Dazu fassen wir die Terme 6xy + 2xy zusammen zu 8xy und setzen danach x = 2 und y = 3 ein.

Das Umformen funktioniert auch bei Potenzen. Diese Potenzen bei Termen kann man ebenfalls zusammenfassen. Die nächste Berechnung zeigt 2x²y³ + 4x²y³ zusammengefasst zu 6x²y³. Wir schreiben dies zunächst mit Malzeichen dazwischen. Im Anschluss setzen wir x = 4 und y = 3 ein. Wichtig beim Rechnen mit Zahlen ist, dass wir zuerst die Potenzen rechnen und danach die Multiplikation.

Anzeige:

Beispiele Termumformung

In diesem Abschnitt sollen weitere Beispiele zur Termumformung gezeigt werden. Dabei werfen wir einen Blick auf die Binomischen Formeln. Wer diese noch nicht kennt kann gerne auch auf den Artikel Binomische Formel sehen.

Beispiel 1:

Wende auf (4y + 3z)² die erste Binomische Formel an.

Lösung:

Die 1. Binomische Formel schreiben wir auf. Dann lesen wir a = 4y und b = 3z aus der Aufgabenstellung ab. Dies setzen wir in a² + 2ab + b² ein und berechnen das Ergebnis damit.

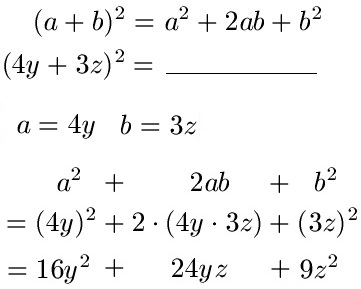
Beispiel 2:

Beispiel Nummer 2 soll den Vorgang umdrehen. Im Prinzip werden die Binomischen Formeln rückwärts angewendet. Verwendet werden soll 16y² + 24yz + 9z². Die 1. Binomische Formel soll darauf angewendet werden.

Lösung:

Wir nehmen die Gleichung und lesen a², 2ab und b² ab. Wir ziehen die mathematische Wurzel und erhalten a = 4y und b = 3z. Damit bauen wir die 1. Binomische Formel auf. Den mittleren Teil kontrollieren wir am Ende der Rechnung noch einmal.

Aufgaben / Übungen Terme umformen

Aufgabe 1: Was ergibt

x + x + x

zusammengefasst?

• 1x
• 2x
• 4x
• 3x

Weiter zur Lösung » Aufgabe überspringen »

Du hast 0 von 6 Aufgaben erfolgreich gelöst.

Anzeigen:

Videos Terme umformen

Fragen mit Antworten zur Termumformung