Schriftlich dividieren / Schriftliche Division

Das schriftliche Dividieren sehen wir uns in den nächsten Abschnitten an. Die Inhalte in Kurzfassung:

• Eine Erklärung, wie das schriftliche Dividieren funktioniert (Einleitung, aber auch mit Rest, mit Komma, mit großen Zahlen).
• Einige Beispiele zum schriftlichen Dividieren.
• Aufgaben / Übungen damit ihr das Thema selbst üben könnt.
• Ein Video zur schriftlichen Division.
• Ein Frage- und Antwortbereich zu diesem Thema.

Dieser Artikel befasst sich allgemein mit der schriftlichen Division. Wer sich jedoch nur für einen Teilbereich interessiert, für den haben wir auch die Themen schriftlich Dividieren mit Rest, schriftlich Dividieren mit Komma oder auch schriftlich Dividieren mit großen Zahlen.

Erklärung schriftlich Dividieren

Wozu braucht man das schriftliche Dividieren?

Starten wir kurz mit den Begriffen. Die Zahl ganz vorne bezeichnet mal als Dividend. Die zweite Zahl bezeichnet mal als Divisor. Das Ergebnis hinter dem "=" nennt man Quotient. Diese Begriffe solltet ihr auswendig lernen, denn sie fallen immer mal wieder. Hier noch einmal als Grafik:

Wir führt man nun eine schriftliche Division selbst durch? Dazu sehen wir uns die Aufgabe von eben mit 735 : 3 noch einmal an.

Beginnen wir mit der Rechnung. Wir haben vorne beim Dividend eine 7 stehen. Nun muss man überlegen, wie oft die 3 - also der Divisor - in die 7 reingeht? Dies geht 2 mal. Wir schreiben die 2 in das Ergebnis.

Danach nehmen wir die 2 aus dem Quotienten (Ergebnis) und multiplizieren wieder mit der 3. Wir erhalten mit 2 · 3 = 6. Diese 6 schreiben wir unter die 7.

Eine Subtraktion steht nun an: Wir berechnen nun 7 - 6 = 1 und schreiben diese 1 darunter.

Wir ziehen die nächste Stelle des Dividenden nach unten. Hier haben wir eine 3.

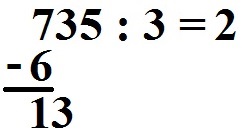
Weiter geht es: Wie oft geht die Zahl 3 in die 13 rein? Antwort: 4 Mal. Diese 4 schreiben wir auch in das Ergebnis.

Erneut multiplizieren wir zurück: Mit 4 · 3 = 12. Diese 12 schreiben wir unter die 13 auf der linken Seite.

Die nächste Subtraktion lautet 13 - 12 = 1. Diese 1 schreiben dir darunter.

Wir ziehen mit der 5 die letzte Stelle runter.

Wie oft geht nun die 3 in die Zahl 15 rein? 5 Mal. Die 5 schreiben wir nun wieder in unseren Quotienten.

Erneut steht eine Multiplikation an: Wir erhalten 5 · 3 = 15. Diese 15 schreiben wir unter die vorherige 15.

Erneut eine Subtraktion: 15 - 15 = 0.

Wir haben nun eine 0 dastehen und keine weitere Stelle beim Dividenden. Wir sind mit der Rechnung dadurch fertig. Mit 735 : 3 = 245 sind wir mit der schriftlichen Division komplett durch.

Anzeige:

Beispiele schriftlich Dividieren

In diesem Abschnitt sollen mehrere Beispiele zum schriftlichen Dividieren vorgerechnet werden. Wir machen dies hier in Kurzform. Die ausführliche Berechnung wird dabei natürlich auch verlinkt.

Beispiel 1:

Manchmal geht eine schriftliche Division nicht "auf". Dann bleibt am Ende ein Rest übrig. Für die Berechnung soll angenommen werden, dass wir 581 Autos haben. Diese sollen gleichmäßig auf 4 Händler verteilt werden. Wie viele Autos bekommt jeder Händler? Was bedeutet der Rest?

Lösung:

Zunächst einmal die Rechnung, im Anschluss wird alles erklärt. Hinweis: Eine Schritt für Schritt Erklärung zu diesem Beispiel findet ihr im Artikel schriftlich Dividieren mit Rest.

So wurde gerechnet:

• In die 4 (Divisor) geht die 5 von ganze vorne genau 1 mal rein. Diese 1 schreiben wir in das Ergebnis.
• Wir multiplizieren zurück: 1 · 4 = 4. Die 4 schreiben wir unter die 5.
• Wir subtrahieren: 5 - 4 = 1. Die 1 schreiben wir hin.
• Wir ziehen mit der 8 die nächste Stelle nach unten. Aus 1 wird 18.
• Wie oft geht die 4 in die 18 rein? Dies geht 4 mal, die 4 schreiben wir in das Ergebnis.
• Wir multiplizieren zurück: 4 · 4 = 16.
• Wir subtrahieren und erhalten 18 - 16 = 2.
• Wir ziehen die nächste Stelle - eine 1 - runter und aus 2 wird 21.
• Die 4 geht in die 21 insgesamt 5 mal rein. Die 5 kommt in das Ergebnis.
• Wir multiplizieren zurück: 5 · 4 = 20.
• Wir subtrahieren: 21 - 20 = 1.
• Es gibt keine weitere Stelle mehr beim Dividend. Die 1 ist damit unser Rest.

Was bedeutet der Rest? In diesem Beispiel wurden 581 Autos auf 4 Autohäuser aufgeteilt. Jedes Autohaus bekommt 145 Autos. Dabei bleibt 1 Auto übrig. Es macht keinen Sinn das Auto in 4 Teile zu zerlegen und zu verteilen. Daher bleibt 1 Auto übrig, welches nicht verteilt werden kann.

Beispiel 2:

Man muss den Rest nicht unbedingt auch als Rest schreiben. Man kann daraus auch eine Kommazahl machen. Wir dies geht zeigt das nächste Beispiel zum schriftlichen Dividieren mit 69,3 : 3. Das Beispiel und auch weitere Aufgaben werden noch einmal ganz ausführlich vorgerechnet in schriftlich Dividieren mit Komma .

So wurde gerechnet:

• Die 3 (Divisor) geht in die 6 ganz vorne 2 mal rein. Dies schreiben wir in das Ergebnis.
• Wir multiplizieren zurück: 2 · 3 = 6.
• Wir subtrahieren 6 - 6 = 0.
• Wir ziehen mit der 9 die nächste Stelle runter. Aus 0 wird 09.
• Wie oft geht die 3 in die 9 rein? Dies geht 3 mal. Die 3 kommt in das Ergebnis.
• Wir multiplizieren mit 3 · 3 = 9.
• Wir subtrahieren mit 9 - 9 = 0.
• Wir erreichen das Komma, daher setzen wir das Komma auch im Ergebnis.
• Wir ziehen mit der 3 die nächste Stelle runter.
• Die 3 geht in die 3 nur 1 mal rein. Wir schreiben die 1 in das Ergebnis.
• Mit 1 · 3 = 3 multiplizieren wir zurück.
• Wir subtrahieren 3 - 3 = 0.
• Keine weitere Stelle mehr, die Berechnung ist komplett.

Aufgaben / Übungen schriftlich Dividieren

Aufgabe 1: Fangen wir ganz einfach an. Berechne 450 : 5 mit der schriftlichen Division.

• 105
• 80
• 100
• 90

Weiter zur Lösung » Aufgabe überspringen »

Du hast 0 von 8 Aufgaben erfolgreich gelöst.

Anzeigen:

Schriftlich Dividieren Video

Fragen und Antworten schriftlich Dividieren