Quadratische Ergänzung

Wie man die quadratische Ergänzung verwendet und wofür man sie braucht, lernt ihr hier. Folgende Inhalte werden angeboten:

• Eine Definition / Erklärung was die quadratische Ergänzung ist.
• Beispiele um Nullstellen und Scheitelpunkt zu bestimmen.
• Übungen damit ihr die quadratische Ergänzung selbst üben könnt.
• Ein Video zur quadratischen Ergänzung.
• Ein Frage- und Antwortbereich zu diesem Thema.

Tipp: Die quadratische Ergänzung ist kein ganz einfaches Thema. Daher macht euch selbst das Leben etwas einfacher. Wenn ihr die folgenden Themen noch nicht kennt, seht bitte erst einmal in diese rein: PQ-Formel und Binomische Formeln. Dies kennt ihr schon? Dann ran an die quadratische Ergänzung.

Quadratische Ergänzung Erklärung

Was ist die quadratische Ergänzung und wozu braucht man diese?

Beginnen wir mit einem ausführlichen Beispiel dazu wie man die quadratische Ergänzung anwendet und die Nullstellen berechnet.

Beispiel 1: Quadratische Ergänzung Nullstellen

Wir haben eine quadratische Gleichung mit 3x² + 9x + 6 = 0. Führe eine quadratische Ergänzung durch und berechne die Nullstellen.

Lösung:

Wir bringen zunächst die quadratische Gleichung auf die Normalform. Dies bedeutet, dass vor x² eine 1 stehen muss. Daher teilen wir durch 3. Die einzelne Zahl (in diesem Fall 6 bzw. dann 2) muss auf die andere Seite der Gleichung gebracht werden.

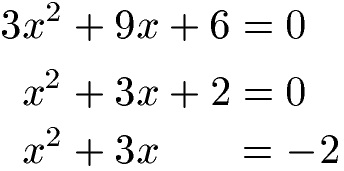
Erinnert ihr euch noch an die 1. Binomische Formel mit a² + 2ab + b² = (a + b)²? Auf die linke Seite der 1. Binomischen Formel versuchen wir nun die linke Seite der Gleichung zu bringen.

Was können wir daraus ablesen? In rot eingerahmt a² = x², in blau eingerahmt 2ab = 3x und b² kennen wir noch nicht. Da a² = x² ist können wir daraus a = x annehmen und dies in 2ab = 3x einsetzen. Dadurch können wir b ausrechnen.

Wir setzen b² = 2,25 in die Gleichung ein. Es handelt sich dabei um eine Gleichung. Fügen wir 2,25 auf der linken Seite der Gleichung ein, müssen wir dies auch auf der rechten Seite machen. Die rechte Seite vereinfachen wir im Anschluss. Wir haben damit quadratisch ergänzt.

Ihr erinnert euch an (a + b)² = a² + 2ab + b²? Und wir wissen von weiter oben das a = x und b = 1,5 ist. Damit formen wir die linke Seite der Gleichung um.

Um nach der quadratischen Ergänzung die Nullstellen zu berechnen, müssen wir noch die Wurzel ziehen. Wichtig: Es handelt sich dabei um die Plusminus-Wurzel wodurch wir zwei Nullstellen erhalten:

Hinweis: Die Nullstellen kann man auch mit der PQ-Formel oder ABC-Formel berechnen. Wie dies mit der PQ-Formel geht sehen wir im Frage- und Antwortbereich am Ende dieses Artikels.

Anzeige:

Quadratische Ergänzung: Beispiel Scheitelpunkt

Die quadratische Ergänzung kann auch zum Berechnen von einem Scheitelpunkt einer quadratischen Funktion verwendet werden. Wie dies geht sehen wir in einem weiteren Beispiel an.

Beispiel 2: Quadratische Ergänzung

Wir haben die folgende Funktion. Führe eine quadratische Ergänzung durch und bestimme damit den Scheitelpunkt.

Lösung:

Wir führen zunächst einen Vergleich mit der 1. Binomischen Formel durch:

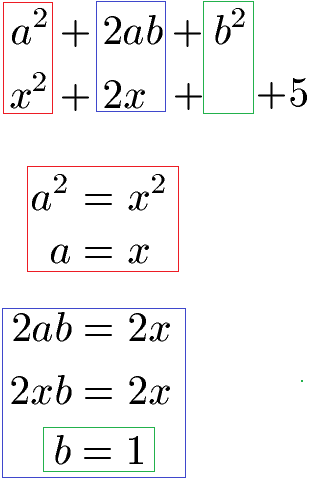
Wir kennen damit b = 1 und können dies in der Ausgangsfunktion ergänzen, in diesem Fall b² = 1. Da wir die Funktion nicht verändern dürfen, müssen wir dies mit 1 wieder ausgleichen. Mit der Binomischen Formel a² + 2ab + b² = (a + b)² können wir die Funktion umformen.

Mit der letzten Gleichung haben wir direkt eine Scheitelpunktform und können direkt den Scheitelpunkt ablesen.

Aufgaben / Übungen quadratische Ergänzung

Aufgabe 1:

Wie lautet die nächste Gleichung nach der quadratischen Ergänzung?

3x² + 9x + 6 = 0

• x² + 3x + 2,25 = 0,25
• x² + 9x + 3,75 = 0,25
• x² + 3x + 1,75 = 0,25
• x² + 3x + 3,75 = 8,25

Weiter zur Lösung » Aufgabe überspringen »

Du hast 0 von 4 Aufgaben erfolgreich gelöst.

Anzeigen:

Video quadratische Ergänzung

Fragen mit Antworten quadratische Ergänzung