Ebene in Parameterform

Die Ebene in Parameterform sehen wir uns hier an. Dies sind die Themen:

• Eine Erklärung, was eine Ebene in Parameterform ist.
• Beispiele für das Aufstellen einer Ebene aus 3 Punkten.
• Aufgaben / Übungen um das Thema selbst zu üben.
• Ein Video zur Ebene in Parameterform.
• Ein Frage- und Antwortbereich zu diesem Gebiet.

Tipp: Es ist hilfreich, wenn ihr bereits wisst, wie man Punkte in ein Koordinatensystem einträgt und was ein Vektor ist. Ansonsten ran an die Ebene in Parameterform.

Ebene in Parameterdarstellung

Stellt euch vor ihr möchtet eine Oberfläche von einem Tisch beschreiben. Mit anderen Worten: Eine Ebene soll beschrieben werden. In der Mathematik kann man dies auf verschiedene Art und Weisen tun. Eine Möglichkeit ist die Parameterform (Parameterdarstellung). Nehmen wir noch einmal den Tisch und zeichnen auf diesem drei Punkte auf:

Wir verbinden jetzt die Punkte A und B sowie A und C. Ich hoffe ich bekomme die Stiftfarbe im Anschluss wieder vom Tisch runter.

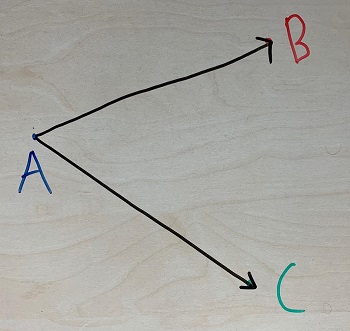
Was für euch wichtig ist: Mit diesen Informationen kann man eine Ebene in Parameterdarstellung beschreiben. Wir sehen uns gleich Beispiele dazu an. Zuvor sehen wir uns noch die allgemeine Darstellung für eine Ebenengleichung an. Diese besteht aus dem Stützvektor p und den Richtungsvektoren (= Spannvektoren) u und v.

Anzeige:

Ebene in Parameterform aufstellen

Sehen wir uns noch ein Beispiel an, wie man eine Ebene in Parameterform aufstellt. Anders ausgedrückt: Eine Ebene in Parameterform aus 3 Punkten soll erzeugt werden.

Beispiel 1: 3 Punkte einer Ebene
Wir haben drei Punkte. Bilde mit diesen eine Ebene in Parameterform.

Lösung:
Wir benötigen zunächst den Ortsvektor vom Koordinatenursprung zum Punkt A. Dies ist jedoch nicht anderes als einfach den Punkt A als Startpunkt zu nehmen. Fehlen uns noch zwei Richtungsvektoren für r und s. Diese erhalten wir, indem wir B - A und C - A Zeile für Zeile berechnen.

Dies eben war noch keine Gleichung, sprich wir haben kein "=". Daher ergänzen wir dies am Anfang noch und rechnen die beiden Richtungsvektoren aus.

Aufgaben / Übungen Ebene in Parameterform

Aufgabe 1:

In diesem Bereich erhaltet ihr die Möglichkeit die Gerade in Parameterform zu üben. Da einige Schüler und Studenten jedoch bereits an einfachen Fragen scheitern, gibt es bei uns auch Fragen zum Thema.

• Mit was kann man eine Ebene beschreiben?

• 3 Punkte
• 1 Punkt
• 2 Punkte
• 1 Punkt, 1 Gerade

Weiter zur Lösung » Aufgabe überspringen »

Du hast 0 von 2 Aufgaben erfolgreich gelöst.

Anzeigen:

Video Ebene in Parameterform

Fragen mit Antworten Ebene in Parameterform